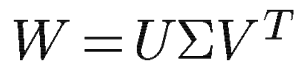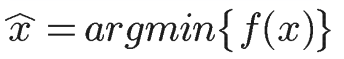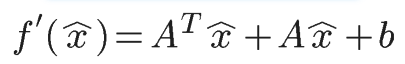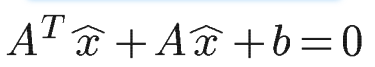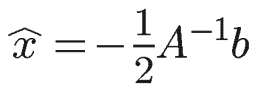目次
- 目次
- はじめに
- 回転行列
- ベクトルの内積
- ベクトルの外積
- 特異値分解
- ヤコビ行列
- ヘッセ行列
- 共分散行列(分散共分散行列)
- 相関行列
- 情報行列(精度行列)
- 行列の二次形式
- 最小二乗法
- 線形代数の基礎
- 参考資料
- MyEnigma Supporters
はじめに
大学の理系学科に進学すると、
まず初めに受ける授業の一つに『線形代数学』があります。
自分も学生時代頑張って勉強していましたが、
一つ大きな疑問がありました。
それは、「これは何に使うのだろう・・・?」
ということです。
固有値や、行列式、ランクなど、
抽象的な知識として学びましたが、
実際にどのようにエンジニアリングに結びつくのかがわからず、
全く興味が持てなかったことを思い出します(笑)。
しかし、大学の研究室でロボティクスの研究をし始めると、
これまで応用例が全く想像できなかった線形代数の知識が、
ふんだんに応用されていることを知りました。
今回は、大学での勉強とは逆の方向として、
それぞれのロボティクスにおける線形代数の応用について
簡単に説明したいと思います。
より詳しい線形代数の知識に関しては、
大学時代の教科書や末尾の参考文献を見てもらえると良いと思います。
回転行列
ロボット工学において、
最も使う行列は回転行列だと思います。
本章では回転行列について概要を説明します。
2次元空間における回転と並進座標変換
ロボットでよく使われる行列演算の代表格として、
2次元空間における、並進と回転による座標変換です。
この座標変換は同次変換とも呼ばれます。
具体的には、あるレーザの観測値をセンサ座標系ではなく、
グローバルな座標系に変換する時などに使用されます。
この同次変換の計算は下記のような、
行列演算で計算できます。
まず、ローカル座標系(センサ座標系)→グローバル座標系

ここで、q_1はセンサ座標系の座標値、
q_2はグローバル座標系の座標値です。
逆にグローバル座標系→ローカル座標系は、

で計算することができます。
3次元空間における回転行列
回転行列は、ある座標点を原点中心で回転させるための行列です。
回転させたい座標値をベクトルに入れて、
回転行列に掛け合わせることによって、
回転後の座標を簡単に計算することができます。
右手座標系において、
x軸、y軸、z軸の回転行列は下記のようになります。

例えば、(x,y,z)=(1,0,0)の点をz軸方向に回転させたい場合は、
下記のようにz軸の回転行列と座標値の列ベクトルを掛け合わせることで、
最終的な回転後の座標値(0,1,0)を取得することができます。

ちなみに上記の回転行列の行列式は常に1になります。
それぞれの軸に対して回転させる場合は、
これらの回転行列をそれぞれ掛け合わせることによって、
3軸の回転を実現できます。
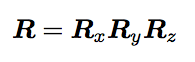
実際に3つの回転行列を掛けあわせた行列は下記のようになります。

一つ重要な点として、
上記の回転行列の掛け合わせる順番は非可換なので注意しましよう。
微小角度変化時の回転行列近似
上記のように3次元の回転行列を3つ掛けあわせた場合、
大量の三角関数が出てくるため、
非常に複雑になり、計算コストも大きくなります。
そこで、回転行列で回転させる角度が微少であると近似できる場合、
sinθ=θ, cosθ=1、θ×φ=0であると近似すると、
先ほどの三次元の回転行列は、
下記のようにシンプルなものに近似できます。

上記の近似回転行列は、
IMUによる3次元速度ベクトルの変換などによく使われます。
ベクトルの内積
ベクトルの内積は二つのベクトルの角度を計算するのに利用することができます。
下記がベクトルの内積の式なので、内積とそれぞれのベクトルのノルムがあれば、
二つのベクトルがなす角度θを計算することができます。

内積そのものは二つのベクトルを行列積で掛け合わせれば計算できます。
また、二つのベクトルが直交する場合は、cos(π/2) = 0なので、
先ほどの内積の定義式から、内積は0になります。
ロボティクスにおいては
衝突判定などに、この内積を利用できます。
ベクトルの外積
ベクトルの外積は、
ある3点で構成される面の
法線方向を計算するのに使うことができます。
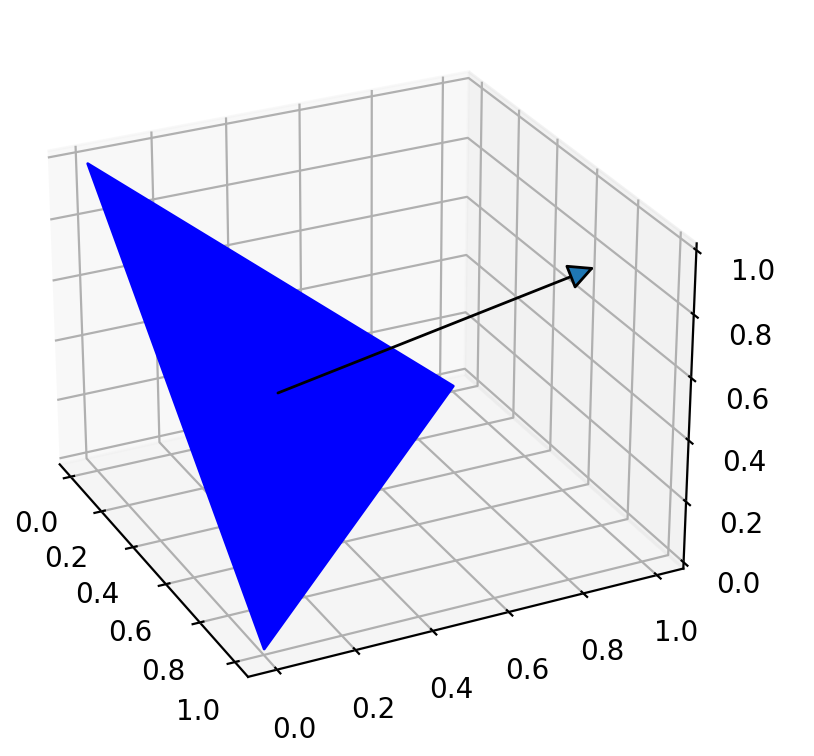
具体的な計算方法としては、
3点のうち一点を選び、
その点から他の二点のまでのベクトルを計算したあと、
その2つのベクトルの外積を計算すると、
3点が構成する平面からの、法線ベクトルが計算できます。
ロボティクスでの応用例としては、
物体の面の法線ベクトルを推定して、
ものを掴む場所を決定したり、
部屋の壁の法線方向を使って、
自己位置推定したり、
壁からできるだけ離れるなどの、
経路生成に利用することができます。
特異値分解
特異値分解はある行列を、
ある特別な行列に分解する手法の一つです。
この特異値分解は下記のような用途でロボティクスでは利用可能です。
Iterative Closest Point (ICP)アルゴリズム
実は、この特異値分解は、
SLAMやScan Matchingという技術でよく使用される
Iterative Closest Point (ICP)アルゴリズムで利用できます。
ICPアルゴリズムを利用したSLAM用MATLABサンプルプログラム - MY ENIGMA
この特異値分解を使用することで、
2つの点群をマッチングさせるための、
片方の点群の移動量を簡単に計算できるようになるのです。
画像圧縮
画像を行列として見立てた時に、
その行列を複数の特徴的な行、列ベクトルの足し合せで表現することで、
画像データのサイズを圧縮することができます。
この特徴的の部分の評価に特異値分解を利用できます。
ヤコビ行列
ヤコビ行列は、複数の関数における
それぞれの変数の偏微分の値を行列として表現したものです。
このヤコビ行列を幾何学的に考えると、
下記の図のように、ある関数のある点における接平面の方向を表しています。
ロボティクスにおいて、このヤコビ行列の応用例は
下記の2つが上げられます。
1. 勾配法による最適化計算
複数の多変数関数における最適化をしなくてはならない場合、
このヤコビ行列が役に立ちます。
このヤコビ行列はある点における接平面の方向なので、
それを使って、勾配を下る方向に探索を行うことで
最小化(最適化)を実現できます。
ヤコビ行列が普通の関数の微分の拡張だと考えると理解しやすいですね。
2. 非線形関数の一次項近似、共分散の遷移
ロボティクスの位置計測における有名な方法に、
拡張カルマンフィルタ(Extened Kalman Filter:EKF)がありますが、
このEKFは非線形性関数の近似として、
ヤコビ行列を使用しています。
EKFでは、このヤコビ行列を使用して、
各Predict, Updateの際の共分散行列の遷移を実現しているのです。
詳しくは下記の記事を参照下さい。
ヘッセ行列
ヘッセ行列(Hessian Matrix)は、
下記のように、
ある関数f(x1,x2,x3..)を、
変数のいずれか2つで微分した式を
それぞれの行列要素にした
行列になります。

上記の式のように、
対角成分は、同じ変数で2回微分した式になり、
また、ヘッセ行列は転置しても同じ行列になります。
このヘッセ行列は、
最適化問題における代表的な主表として、
ニュートン法などで利用されます。
共分散行列(分散共分散行列)
ロボティクスにおいて、共分散行列は頻繁に出てきます。
カルマンフィルタを使用して、位置を推定した場合、
その位置の状態ベクトルと、その推定の精度として
共分散行列(分散共分散行列)が推定されます。
拡張カルマンフィルタを使用した自己位置推定MATLABサンプルプログラム - MY ENIGMA
この共分散行列の値を使うと、
推定精度の楕円を描画することができます。
カルマンフィルタにおける誤差楕円の計算方法 - MY ENIGMA
共分散とは、ある二組のデータの各平均からの偏差の平均(期待値)です。
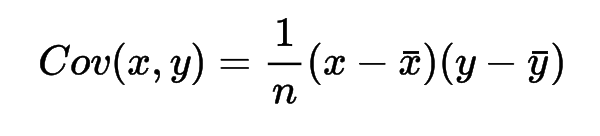
(分散)共分散行列は各組の共分散を行列として格納したものです。
この共分散行列の対角成分は同じ変数の偏差の積の平均(期待値)なので、
通常の各変数の分散になります。
ですので、共分散行列の対角成分は必ず正の値になります。
また非対角成分は、それぞれの変数の共分散です。
この共分散行列の上対角成分と下対角成分は、
各変数の平均の偏差を交換したものなので、
掛け算の左右の項を交換しても、
値が変わらないことを考えると、
共分散行列の上対角成分と下対角成分は同じ値になります。
また、この共分散の値はそれぞれの変数の平均の偏差の掛け算なので、
正と負の両方の値をとります。
正の値の場合、片方の値が大きくなると、もう片方の値も大きくなる傾向にあり、
負の値の場合、片方の値が大きくなると、もう片方の値は小さくなる傾向にあります。
共分散行列の詳しい説明は下記の資料を参考にされると良いと思います。
相関行列
相関行列は上記の共分散行列を標準化したものになります。
i行,j列の共分散の項をs_ijとすると、
その項に対応する相関行列の項r_ijは下記の式で計算されます。

つまり、それぞれの共分散の項を対応する変数の標準偏差で割ったものになります。
共分散行列の対角成分が各変数の分散であることを考えると、
それらの値を標準化する相関行列では、対角成分は1になります。
また、非対角成分は相関係数になります。
従って、非対角成分の値が、
1に近いほど、片方の値が大きくなると、もう片方の値も大きくなる傾向にあり、
-1に近いほど、片方の値が大きくなると、もう片方の値は小さくなる傾向にあります。
情報行列(精度行列)
情報行列は共分散行列の逆行列です。
この情報行列は、フィッシャーの情報行列や、
精度行列(Precision Matrix)とも呼ばれます。
共分散行列の代わりにこの情報行列を使用するフィルタを、
情報フィルタといいます。
この情報行列を使用することにより、
大量の状態量を推定したいSLAMのような問題において、
計算コストを非常に小さくすることができます。
行列の二次形式
ロボティクスにおける重要なアルゴリズムの中には、
二次形式の形で書き表せるものが多いです。
二次形式は、二次関数の行列版だと言えますが、
一般的には下記のような形をしています。
ここでx,A,b,cはすべてのベクトルか行列になります。
例えば、下記の記事のようにベイズフィルタの
共分散の遷移は二次形式で書き表すことができますし、
拡張カルマンフィルタを使用した自己位置推定MATLABサンプルプログラム - MY ENIGMA
あるよくわからない関数を、
局所的に二次形式で近似するとかが実用例だと思います。
また、色々な文献を読んでいると、この二次形式が出てくるのですが、
多くの研究者が、何故わざわざ二次形式であることを強調するのかが
わかりませんでした。
それには実は理由があったのです。
それは
『二次形式の式は最適化がしやすい』
ということです。
ロボティクスでは、何かの認識する時に、
誤差を最小化したり、
確率(尤度)を最大化したりするのがお決まりですが、
二次形式ではそれが意外と簡単にできます。
では、先ほどの二次形式の式f(x)を最大化してみましょう。
f(x)を最小化(or -f(x)を最大化)することを考えると,
となるような\hat{x}を求めることになります。
そこで、よくやる方法として、
最小値 or 最大値となる、いわゆる極値は
となることを考えます。
そこで、f(x)を微分すると
となるので、f'(\hat{x})=0とすると
となって、これを整理すると
そして、左辺をxのみにすると
となります。
ここで、ロボティクスで使用される二次形式の式の
大部分に当てはまるのですが、行列Aが対称行列である場合、
となり、非常に簡単な式で極値を計算できることがわかります。
以上のように二次形式で目的のシステムを近似することにより、
簡単に極値を計算できる特性を利用して、
様々な最適化計算をすることができます。
また、xTQxのような形式そのものを二次形式と呼ぶ場合があります。
この二次形式を||x||^2_Qと記述する場合もあります。
ここで、x=0以外のすべてに対して上記のxTQx>0である場合、
この二次形式は正定(positive definite)と呼びます。
またxTQx>0である場合、半正定(positive semi-definite)といいます。
加えて、この二次形式をV=xTQxとした時、
このVの勾配⊿Vは、
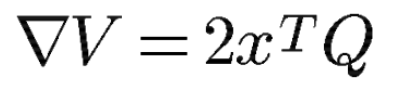
で計算できます。
二次形式の利用用途
この二次形式は、ロボティクスにおいて、
複数の状態量を推定するカルマンフィルタや、
最適化手法である二次計画法
最適化問題を利用して制御するモデル予測制御
などで利用されます。
最小二乗法
あるコスト関数を最小化する入力を計算する
最小二乗法も線形代数の知識が必要です。
ロボティクスでは、
パラメータの同定や、モデル予測制御、
多項式フィッティングによるパス生成など、
様々な用途で最小二乗法は使用されます。
最小二乗法に関しては、下記を参照ください。
線形代数の基礎
上記の内容をより基礎的な部分から勉強したい場合は、
下記の記事を参照ください。
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com