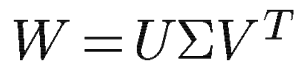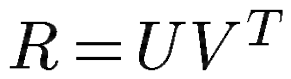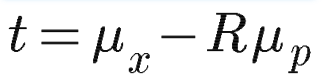はじめに
Iterative Closest Point: ICPアルゴリズムは、
レーザやステレオカメラなどて取得した点群データ(Point Cloud)
の二セット分のデータを使用して、
それらの点群が一番マッチングする位置
を計算するアルゴリズムです。
もう少し詳しく言うと、
片方の点群をもう片方の点群に最もフィットするために、
片方の点群をどれだけ移動すればよいかを
計算します。
このICPは、ある物体を複数の方向から観測(撮影)して、
その物体の形状を復元する
『Structure From Motion』という手法に利用されたり、
(下図はStructure From Motionによる建物の復元)
ロボットに搭載されているレーザの観測点を
2つの時間でマッチングさせ、
その移動量を計算することで、
Wheel Odometryの代わりに使ったりすることが多いです。
差動二輪型ロボットのWheel Odometryによる自己位置推定プログラム - MY ENIGMA
今回は、このICPアルゴリズムのMATLABと
Pythonのサンプルコードを作成したので、
公開したいと思います。
特異値分解(SVD)を用いたICP
下記の参考文献のFreiburg大学の資料にある通り、
点と点の対応が既知の場合は、
ICPアルゴリズムは非常に単純に実装できます。
それが、特異値分解(Singular Value Decomposition:SVD)を利用したものです。
特異値分解は、ある行列を特別な行列に分解する線形代数の方法の一つですが、
この特異値分解を使用すると、簡単に各スキャン点のノルム誤差を最小にするような
移動量(並進ベクトルt,と回転行列R)を計算できます.
なぜ特異値分解を使用すると移動量を計算することができるのか、
に関しては参考資料3を見ていただけるとわかると思います。
簡単にアルゴリズムを説明すると、
1. 各点群の重心を計算して、各点の座標を重心中心に変換する
2. その座標行列を互いに掛けあわせたWという行列を特異値分解する
3. 特異値分解によって得られたUとVを使って、
各点のノルム誤差を最小にするtとRは下記の式で計算できる。
ここで、\mu_xと\mu_pはそれぞれの点群の重心座標です。
4 1-3を繰り返して、収束するまで計算をする。
プログラムとして実装するのは意外と簡単ですね。
今回公開するサンプルコードは
この特異値分解による最適化計算の部分を実装してみたものです。
サンプルMATLABコード
下記のGitHubリポジトリにて公開しています。
MATLABRobotics/SLAM/ICP/ICPsample.m at master · AtsushiSakai/MATLABRobotics
プログラムを起動すると、
下記のようなグラフと、
推定結果がコマンドウィンドウに表示されるはずです。
青の点を緑の点にピッタリ合わせるような
Rとtを計算して、それで変換したのが、赤の点といった感じです。
並進移動量は0.001m以下、角度も1deg以下の精度で推定できていることが、
コマンドウィンドウの結果からわかると思います。
Pythonサンプルコード
下記のリポジトリで同じICPアルゴリズムを
Pythonで実装したものを公開しています。
上記のコードを実行すると、
記事冒頭のICPによるシミュレーションが実施されます。