目次
- 目次
- 最急降下法について
- 最急降下法の注意点
- MATLABサンプルプログラム
- Pythonサンプルプログラム
- Armjio(アルミホ条件)とバックトラック法による学習パラメータ線形探索
- シミュレーションで使用したコスト関数
- 参考資料
最急降下法について
最急降下法は、関数の微分情報を使った非線形最適化の手法の中で
最もシンプルなものの一つです。
非線形モデルの偏微分行列であるヤコビ行列を使って、
勾配方向にパラメータを更新することで、
最適化を実施します。
(ヤコビ行列に関しては、下記の記事を参考してもらえると良いと思います。
パラメータの更新式は下記の通りです。
ちなみにαは学習パラメータと呼ばれ、
良く使用される方法としては、
事前に決めた一意のパラメータを利用するか、
黄金分割法や、後述のアルミホ条件によるバックトラック法の直線探索法を使って
最適なαを逐次決定します。
最急降下法の注意点
通常の場合、
最急降下法で最適化解を得ることができますが、
下記のグラフのように、
ある方向では極小値だが、
ある方向では極大値である
いわゆる鞍点(あんてん)の場合、
この点に収束してしまう可能性があります。

この鞍点に収束しているかどうかを
確認する場合は、
この点におけるヘッセ行列が正定か準正定かどうかを、
確認すればOKです。
ちなみに、正定かどうかの確認は、
ヘッセ行列Hの固有値がすべて正か、
または、下記の二次形式の式がすべてのxにおいて、
正であることが条件になります。
MATLABサンプルプログラム
% ------------------------------------------------------------------------- % % File : SteepestDescentMethod.m % % Discription : Non-Linear optimizion with Steepest Descent Method % % Environment : Matlab % % Author : Atsushi Sakai % % Copyright (c): 2014 Atsushi Sakai % % License : Modified BSD Software License Agreement % ------------------------------------------------------------------------- function [] = SteepestDescentMethod() close all; clear all; disp('Optimization simulation with Steepest Descent method starts!!') %シミュレーション空間の最大最小範囲 maxxy=5; minxy=-5; %メッシュデータの生成 [x1range,x2range,yrange]=CreateMeshData(minxy,maxxy); %初期パラメータの生成[x1 x2 y] param=InitSearchParameter(minxy,maxxy); finalParam=SteepestDescentMethodOptimization(param,x1range,x2range,yrange); function finalParam=SteepestDescentMethodOptimization(param,x1range,x2range,yrange) %最急降下法による最適化 iterationMax=50;%イタレーションの最大回数 alpha=0.01;%学習率 result=[];%パラメータの履歴 for i=1:iterationMax %ヤコビ行列の取得 J=CalcJacobi(param(1),param(2)); %最急降下法によるパラメータの更新 param(1:2)=param(1:2)-alpha*J; param(3)=f(param(1),param(2)); if sum(abs(alpha*J))<=0.01 disp('Converge'); i break; end %シミュレーション結果の描画 figure(1) hold off; contour(x1range,x2range,yrange,100); hold on; result=[result;param]; plot3(result(:,1),result(:,2),result(:,3),'.-k','markersize',10); xlabel('x1'); ylabel('x2'); view(2) drawnow; pause(0.5); end finalParam=param(end,:); function param=InitSearchParameter(minxy,maxxy) %初期パラメータを作成する関数 x1=maxxy - (maxxy-minxy).*rand(1,1); x2=maxxy - (maxxy-minxy).*rand(1,1); y=f(x1,x2); param=[x1' x2' y']; function [x1range,x2range,yrange]=CreateMeshData(minxy,maxxy) %シミュレーション空間のメッシュデータを作成する関数 %メッシュデータの作成 [x1range,x2range]=meshgrid(minxy:0.3:maxxy); yrange=f(x1range,x2range); function y = f(x1,x2) % Himmelblau's function % see Himmelblau's function - Wikipedia, the free encyclopedia % http://en.wikipedia.org/wiki/Himmelblau%27s_function y=(x1.^2+x2-11).^2+(x1+x2.^2-7).^2; function J= CalcJacobi(x,y) % jacobi matrix of Himmelblau's function dx=4*x^3+4*x*y-44*x+2*x+2*y^2-14; dy=2*x^2+4*x*y+4*y^3-26*y-22; J=[dx dy];
MATLABのサンプルプログラムは
下記のGitHubリポジトリで公開されています。
MATLABRobotics/SteepestDescentMethod.m at master · AtsushiSakai/MATLABRobotics
Pythonサンプルプログラム

下記がPythonサンプルプログラムです。
import matplotlib.pyplot as plt import numpy as np import random def Jacob(state): """ jacobi matrix of Himmelblau's function """ x = state[0] y = state[1] dx = 4 * x ** 3 + 4 * x * y - 44 * x + 2 * x + 2 * y ** 2 - 14 dy = 2 * x ** 2 + 4 * x * y + 4 * y ** 3 - 26 * y - 22 J = np.array([dx, dy]) return J def HimmelblauFunction(x): """ Himmelblau's function see Himmelblau's function - Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Himmelblau%27s_function """ return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2 def CreateMeshData(minXY, maxXY, delta): x = np.arange(minXY, maxXY, delta) y = np.arange(minXY, maxXY, delta) X, Y = np.meshgrid(x, y) Z = [HimmelblauFunction([x, y]) for (x, y) in zip(X, Y)] return X, Y, Z def SteepestDescentMethod(start, Jac, alpha=0.001): """ Steepest Descent Method Optimization """ result = start x = start while 1: j = Jac(x) sum_j = np.abs(j).sum() if sum_j <= 0.01: print("OK") break x = x - alpha * j result = np.vstack((result, x)) return result def main(): delta = 0.1 minXY = -5.0 maxXY = 5.0 nContour = 50 start = np.array([random.uniform(minXY, maxXY), random.uniform(minXY, maxXY)]) (X, Y, Z) = CreateMeshData(minXY, maxXY, delta) plt.contour(X, Y, Z, nContour) plt.plot(start[0], start[1], "xr") opt_history = SteepestDescentMethod(start, Jacob) optX = [x[0] for x in opt_history] optY = [x[1] for x in opt_history] plt.plot(optX, optY, "-b", label=f"Without Line Search: (Iter:{len(opt_history)})") plt.legend() plt.show() if __name__ == '__main__': main()
Armjio(アルミホ条件)とバックトラック法による学習パラメータ線形探索
最急降下法は、
前述の通り、ヤコビ行列によって勾配方向を計算できますが、
学習パラメータも適切に設定しないと、
小さすぎる場合は、最適値までの探索回数が多くなり、
大きすぎる場合は、最適値を飛び越えてしまい、収束しなくなってしまいます。
そこで、最急降下法の学習パラメータαを適切に決定するための手法として、
Armijo(アルミホ条件)とバックトラック法による
学習パラメータ線形探索がよく利用されます。
Armijo条件は、適切なαを決定するための条件で、
下記の不等式を満たすαを良い学習パラメータと判断する方法です。

ここで、g(α)は学習パラメータがαの時のコストの値、
dはヤコビ行列、τは定数パラメータです。
g'(α)は、下記のように計算されるため、

代入すると、下記で計算できます。
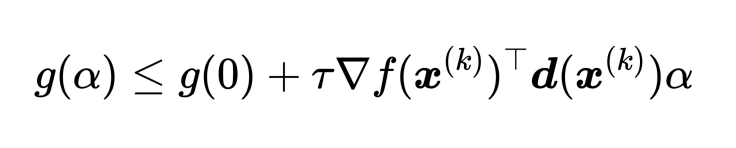
ここで、最急降下法の場合、探索方向dと⊿fは下記のような反対方向の関係があるため、
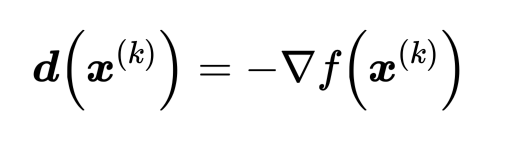
最終的な判定式はこちらのようになります。

この条件式は、α=0のコスト値を切片とした線分よりも
下にコスト値が来る場合を、良い学習パラメータだと判断しています。
この条件に関しては下記の記事を参照ください。
バックトラック法は、αの初期値を1とし、
0<β<1のβを使って、下記の式で

αを徐々に小さくしていくことで、
αを探索する方法です。
大きい値が徐々に小さくなるように
探索するため、Armijo条件では
αが0に限りなく小さくても、
条件を満たしてしまう問題を解決できます。
下記が通常の定数の学習パラメータの最急降下法と、
Armjio(アルミホ条件)とバックトラック法による学習パラメータ線形探索を利用した、
最急降下法を比較するPythonコードです。
import matplotlib.pyplot as plt import numpy as np import random def Jacob(state): """ jacobi matrix of Himmelblau's function """ x = state[0] y = state[1] dx = 4 * x ** 3 + 4 * x * y - 44 * x + 2 * x + 2 * y ** 2 - 14 dy = 2 * x ** 2 + 4 * x * y + 4 * y ** 3 - 26 * y - 22 J = np.array([dx, dy]) return J def HimmelblauFunction(x): """ Himmelblau's function see Himmelblau's function - Wikipedia, the free encyclopedia https://en.wikipedia.org/wiki/Himmelblau%27s_function """ return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2 def CreateMeshData(minXY, maxXY, delta): x = np.arange(minXY, maxXY, delta) y = np.arange(minXY, maxXY, delta) X, Y = np.meshgrid(x, y) Z = [HimmelblauFunction([x, y]) for (x, y) in zip(X, Y)] return X, Y, Z def SteepestDescentMethod(start, Jac, alpha): """ Steepest Descent Method Optimization """ result = start x = start while 1: j = Jac(x) sum_j = np.abs(j).sum() if sum_j <= 0.01: print("OK") break x = x - alpha(HimmelblauFunction, j, x) * j result = np.vstack((result, x)) return result def main(): delta = 0.1 minXY = -5.0 maxXY = 5.0 nContour = 50 start = np.array([random.uniform(minXY, maxXY), random.uniform(minXY, maxXY)]) (X, Y, Z) = CreateMeshData(minXY, maxXY, delta) plt.contour(X, Y, Z, nContour) plt.plot(start[0], start[1], "xr") def constant(func, grad, x): return 0.001 opt_history = SteepestDescentMethod(start, Jacob, constant) optX = [x[0] for x in opt_history] optY = [x[1] for x in opt_history] plt.plot(optX, optY, "-b", label=f"Without Line Search: (Iter:{len(opt_history)})") def armijo_line_search(func, grad, x, beta=0.9, tau=0.3): alpha = 1.0 while func(x - alpha*grad) > (func(x) - tau*alpha*np.dot(grad, grad)): alpha *= beta return alpha opt_history = SteepestDescentMethod(start, Jacob, armijo_line_search) optX = [x[0] for x in opt_history] optY = [x[1] for x in opt_history] plt.plot(optX, optY, "-r", label=f"Armijo Line Search (Iter:{len(opt_history)})") plt.legend() plt.show() if __name__ == '__main__': main()
上記のコードを実行すると、下記のように
線形探索ありなしで、最適化を実施し、比較でき、
線形探索を実行することで探索回数を大幅に減らすこと
ができていることがわかります。

シミュレーションで使用したコスト関数
今回のシミュレーションでは、Himmelblau関数を使いました。
Himmelblau's function - Wikipedia, the free encyclopedia
Himmelblau関数のヤコビ行列は下記の通りになります。
参考資料
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
# MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。

