目次
- 目次
- Model Predictive Control:モデル予測制御とは?
- MPCの歴史
- MPCの種類
- Receding Horizon 制御
- モデル予測制御の利点
- モデル予測制御の欠点
- モデル予測制御の応用例
- MPCを実装するフロー
- PythonによるシンプルなMPC制御シミュレーション
- 最適化コードジェネレータによるモデル予測制御の高速化
- モデル予測制御における制約条件の緩和
- モデル予測制御におけるパラメータ
- シンプルなMPCの数式の導出
- Math WorksのMPC入門ビデオ
- より深くモデル予測制御を学ぶために
- 参考資料
- MyEnigma Supporters
Model Predictive Control:モデル予測制御とは?
Model Predictive Control:モデル予測制御は、
現代制御アルゴリズムの一つで、
事前に設定したシステムモデルに基づいて、
逐次的に最適化問題を解くことで
制御入力を決定する手法です。

Model Predictive Controlの頭文字を取って、
MPCと呼ばれることも多いようです。
MPCの歴史
MPCは1970年代に石油精製や化学プラントのような
制御ループが比較的遅いが、システムの遅れが大きいシステム用の
制御アルゴリズムとして開発されました。
当時はMPCという名前で統一されていたわけではなく、
Dynamic Matrix Controlや、
Model Predictive Heuristic Controlなどと呼ばれていました。
その後、2000年ぐらいまでは、
上記以外のプロセス制御系の制御に利用されていましたが、
その後、コントローラの計算性能の向上と、
最適化問題を解くソフトウェア(ソルバー)の進化により、
制御ループが高速な、
リアルタイム制御システムにまで応用が広がっています。
MPCの種類
前述の通り、
MPCは制御のシステムモデルと、最適化アルゴリズムを
組み合わせた制御システムですが、
使用するシステムモデルと最適化アルゴリズムに応じて、
二種類に分類されます。
一つ目は、システムモデルが線形モデルであり、
制約条件が凸関数や凸空間で表せる場合、
MPCの制御問題は凸最適化アルゴリズムで解くことができます。
このようなMPCを線形MPCといい、
一般的にMPCというとこの線形MPCのことを指します。
本記事では基本的にこの線形MPCのことを述べます。
線形MPC以外のMPCに関しては、下記の記事を参照ください。
Receding Horizon 制御
モデル予測制御の考えの中で、
現在からある未来の時間までの
一定時間の制御出力プロファイルを最適化により計算し、
そのプロファイルの初めの値のみを制御に利用する手法を
Receding Horizon制御といいます。
現在実用化されているMPCのシステムの殆どが、
このReceding Horizon制御のアイディアを使っているため、
MPCとReceding Horizon制御(:RH制御)を
同じものとして扱っている場合も多いようです。
下記の図は、一般的なRH制御のシステムダイアグラムです。
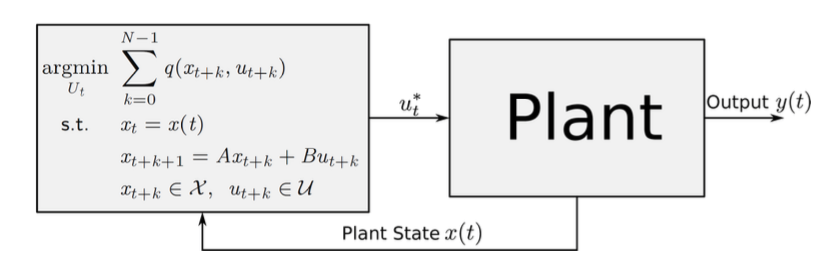
左のブロックがMPCコントローラーであり、
qはMPCの評価関数、xは状態変数、uは入力値を表します。
時刻tの時の状態変数をx(t)とし、
モデルは線形システムを前提とすることが多いようです。
最後の行は、状態xや入力uの制約条件を表しています。
下記の図は、RH制御の時刻t,t+1の時の
入力プロファイルと
出力プロファイルを表したものです。

RH制御では、
出力プロファイルの推定時間長さを
予測ホライズン:Npといい,
入力プロファイルの推定長さは、
制御ホライズン:Nmといいます。
一般的に、Nm < Npのように、
予測ホライズンよりも、
制御ホライズンは短くすることが多いようです。
なぜなら制御ホライズンが長いと、
最適化の変数が多くなってしまい、
最適化が不安定になるからです。
また予測ホライズンが短いと、
出力の推定時間が短いため、
制御が不安定になりやすくなります。
制御ホライズンが短いことにより、
推定できない予測ホライズンの区間は、
上記の図のように最後の入力が一定であるという仮定のもと、
予測値を推定します。
このNmとNpの決め方としては、
初期値として、Nmは2~3の値を、
Npの値は制御の時定数分の値を設定することが多いようです。
モデル予測制御の利点
モデル予測制御には、
他の制御手法と比べて、
大きく分けて3つの利点があります。
利点1:入力や出力の制約条件をシステマチックに扱うことが可能
一般的に、対象とする制御システムの入力や出力には、
制約条件というものがあります。
例えば、
車両の場合、加速度の限界値や、
安全性の面での速度の最大値、
ステアリングの最大角度や最大変化量などです。
他にもトルクの最大値や、
電圧、電力の最大値や最小値など、
現実世界における制御システムを考えた場合に、
制約条件の無い入出力は殆ど無いと思われます。
モデル予測制御では、
ラグランジュの未定乗数法などを使って、
このような制約条件を最適化の際に取り込むことにより、
制約条件を正確に考慮した上で、
精密な制御を実施することができます。
ラグランジュの未定乗数法に関しては、
下記の記事を参照下さい。
利点2:多入力多出力のシステムの制御に利用しやすい
一般的な制御システムは、
多入力多出力のものが多いです。
従来の制御手法では、
そのような多入力多出力の制御システムを
一つの制御システムとして取り扱うのが難しいという問題がありました。
そこで良く使用される手法が、
複数の制御ループを組み合わせて
一つの制御システムを構築することですが、
これだと、システムとしての全体最適が困難であったり、
一つのコントローラーに制御システムを
まとめるのが難しいという問題がありました。
モデル予測制御制御では、
多入力多出力のモデルを構築することで、
一つの制御システムで
多入力多出力の制御を実現することができます。
これにより制御システムの全体最適を実現した、
制御システムを実現できます。
利点3:高い制御性能が期待できる
前述のように、
モデル予測制御ではシステム全体の制約条件や、
複数の入力出力を考慮したモデルを利用することで、
最適制御を実施するため、高い制御性能が期待できます。
加えて、前述の通りモデル予測制御は、
フィードバック制御の機能も有しているため、
外乱などにも強く、実用性の高い制御を実現することができます。
利点4: 時間遅れ補正を明示的に考慮することができる
MPCでは各時刻毎の将来の振る舞いを予測して、
制御を実施するため、
制御や入力の時刻遅れを明示的に考慮することができます。
利点5: パラメータの自動チューニング手法が存在している。
コントローラの性能をできるだけ高めるには、
コントローラのパラメータをチューニングすることは不可欠ですが、
MPCでは、LQRなどの最適制御のパラメータチューニングと同じ方法を使うことで、
自動的にパラメータチューニングする手法が存在します。
モデル予測制御の欠点
上記のように、モデル予測制御には
既存の制御手法には無い、
様々な利点がありますが、
やはり欠点もいくつかあります。
欠点1: 計算が重い
モデル予測制御は最適化計算を
毎制御ループ毎に計算する必要があるため、
計算が重いという問題があります。
よって、高速な応答性が必要な
制御システムには利用しずらいという問題があります。
近年はコンピューターの性能が向上してきているため、
問題にならないこともありますが、
やはり最適化のロジックなどは
高速なものを利用する必要があります。
欠点2: 閉ループ安定性は必ず約束されない
有限時間の間のみ考慮して、
制御入力を計算しているため、
必ずしも制御システムが安定であるとは限りません。
MPCでは、この安定性をできるだけ担保するように
システムを設計するのが重要になります。
欠点3: 線形モデルを設計する必要がある。
上記のモデルの図にあるように、
MPCで制御する対象は線形モデルで記述される必要があります。
制御する対象が非常に複雑であったり、非線形であったりすると、
この線形モデルを作るのが難しい場合があります。
この線形化モデルは、
基本的に物理や幾何学関係により設計するのが一般的ですが、
様々な入力と出力により、ニューラルネットや機械学習により
線形モデルを生成する方法もあるようです。
モデル予測制御の応用例
下記記事を参照下さい。
MPCを実装するフロー
MPCを実際に実装する場合は、
下記のようなフローをとることが多いようです。
1. 線形モデルを構築する
前述の通り、MPCは基本的にシステムのモデルを
線形システムでモデリングします。
前述の通り、このモデリングには
力学的、幾何学的な関係を使ってモデリングをしたり、
機械学習などでモデリングする方法があるようです。
2. 凸最適化のツールを選定する
MPCでは一般的に、
コスト関数の最適化に凸最適化の技術を利用します。
この凸最適化を自力で実装する方法もありますが、
最近は凸最適化のツールが様々な言語で実装されているので、
自分の利用したい環境に合わせて、
ツールを選定するのが便利かと思います。
凸最適化の概要やツールに関しては、
下記の資料を参照下さい。
PythonによるシンプルなMPC制御シミュレーション
Pythonの最適化モデリングツールであるCVXPYを使って
簡単なMPCの制御シミュレーションをしてみたいと思います。
まず、制御状態をx,入力をuとし、
モデルを線形方程式で表せるとすると、
下記の式を満たす入力u0...uT-1を最適化で計算します。
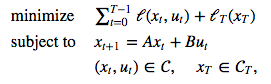
ここでlはコスト、lTは終端コストです。
CとCtはそれぞれ、状態と入力、終端値に対する制約条件になります。
今回解く問題は、状態は4次元、
入力の次元は2次元、
予測ホライゾンは50個
線形モデルのパラメータと状態量の初期値は乱数で与えています。
コストとしては、xの二乗和とuの二乗和としました。
各時刻における線形モデルと、
各入力に1以下という制約を入れてます。
また終端の制約として、初期値をx_0, 最終値を0にするように制約を入れます。
下記がシミュレーションコードです。
#! /usr/bin/python # -*- coding: utf-8 -*- u""" Simple Model Predictive Control Simulation author Atsushi Sakai """ import time from cvxpy import * import numpy as np import matplotlib.pyplot as plt print("Simulation start") np.random.seed(1) n = 4 #state size m = 2 #input size T = 50 #number of horizon #simulation parameter alpha = 0.2 beta = 5.0 # Model Parameter A = np.eye(n) + alpha*np.random.randn(n,n) B = np.random.randn(n,m) x_0 = beta*np.random.randn(n,1) x = Variable(n, T+1) u = Variable(m, T) states = [] for t in range(T): cost = sum_squares(x[:,t+1]) + sum_squares(u[:,t]) constr = [x[:,t+1] == A*x[:,t] + B*u[:,t], norm(u[:,t], 'inf') <= 1] states.append( Problem(Minimize(cost), constr) ) # sums problem objectives and concatenates constraints. prob = sum(states) prob.constraints += [x[:,T] == 0, x[:,0] == x_0] start = time.time() result=prob.solve(verbose=True) elapsed_time = time.time() - start print ("calc time:{0}".format(elapsed_time)) + "[sec]" if result == float("inf"): print("Cannot optimize") import sys sys.exit() f = plt.figure() ax = f.add_subplot(211) u1=np.array(u[0,:].value[0,:])[0].tolist() u2=np.array(u[1,:].value[0,:])[0].tolist() plt.plot(u1,'-r',label="u1") plt.plot(u2,'-b',label="u2") plt.ylabel(r"$u_t$", fontsize=16) plt.yticks(np.linspace(-1.0, 1.0, 3)) plt.legend() plt.grid(True) plt.subplot(2,1,2) x1=np.array(x[0,:].value[0,:])[0].tolist() x2=np.array(x[1,:].value[0,:])[0].tolist() x3=np.array(x[2,:].value[0,:])[0].tolist() x4=np.array(x[3,:].value[0,:])[0].tolist() plt.plot(range(T+1), x1,'-r',label="x1") plt.plot(range(T+1), x2,'-b',label="x2") plt.plot(range(T+1), x3,'-g',label="x3") plt.plot(range(T+1), x4,'-k',label="x4") plt.yticks([-25, 0, 25]) plt.ylim([-25, 25]) plt.ylabel(r"$x_t$", fontsize=16) plt.xlabel(r"$t$", fontsize=16) plt.grid(True) plt.legend() plt.tight_layout() plt.show()
上記のコードを実行すると、
下記のグラフが表示されます。

上記のグラフを見ると分かる通り、
入力のuの値の制約条件がきちんと守られていることがわかります。
またその入力で4つの状態量のすべてが0に収束していることがわかります。
きちんとMPCで制御できているようです。
ちなみに前述のように、
実際のMPCでは、この最適化を毎回実施し、
入力プロファイルの初めのデータのみを制御に利用します。
またx0の値を毎回センサなどの観測値を使って
更新しながら制御する形になります。
最適化コードジェネレータによるモデル予測制御の高速化
上記のcvxpyを使うと、
簡単にモデル予測制御コントローラを実装出来ますが、
実際のシステムでMPCのコントローラを使いたい場合は、
パフォーマンスを向上させるために、
C言語などで再実装する必要があります。
そんな時に便利なのが、
最適化コードジェネレータです。
これは、モデリング言語で最適化問題を記述すると、
その問題を高速に解くC言語コードを自動生成してくれます。
最適化コードジェネレータとしては、
cvxgenや
Forces Proが有名です。
モデル予測制御における制約条件の緩和
MPCを実際のシステムに利用する場合に問題になるのが、
外乱や、制約条件が厳しい時に
最適化計算が不可能(Infeasible problem)になることです。
この問題の対策として、
前回計算された入力プロファイルのt=2を利用する方法や、
最も重要でない制約条件を緩和する方法があります。
2つ目の制約条件を緩和する方法では、
緩和しない制約条件(ハード制約)といい、
緩和する制約条件を(ソフト制約)といいます。
このソフト制約は、基本的にはハード制約として振る舞いますが、
どうしても計算が出来ない場合は、
制約を超えることを許容するようになります。
一般的にMPCにソフト制約を入れる場合は、
入力の制約は超えることができないので、
出力の制約をソフト制約にすることが多いようです。
このソフト制約を実現するには、
スラック変数(slack variable)という疑似変数を
追加することで実現できます。
スラック変数の追加方法に関しては、
下記を参照下さい。
モデル予測制御におけるパラメータ
MPCには様々な定式化の方法がありますが、
下記の式を一般的な形とすると、

いくつかチューニングすべきパラメータがあります。
1 状態変数のコスト行列Q
状態変数のコスト行列Qは、
各状態変数の重みパラメータです。
状態変数の一つを最小化したい場合は、
その部分の重みを大きくします。
このQは基本的には正対称行列です。
また、上記の式ではすべての予測時間において、
Qが同じ値を使っていますが、
MPCの手法によっては、予測時間に応じてQを変える
手法もあるようです。
加えて、ホライゾンの最後のコスト行列だけを
大きくすることが多いため、上記の式のように、
別途Qfinalというコスト行列を設定することが多いようです。
これは、終端の制約条件をつけると、
システムの安定性が保証されるのですが、
制約条件にすると、解が無くなることがあるため、
大きな重みを付けて、コスト関数に入れることが多いようです。
2. 入力のコスト行列 R
入力のコスト行列Rは、
入力の量を抑制するための重みパラメータです。
このパラメータを大きくすることで、
システムの安定性が向上します。
しかし、外乱に対する復帰が遅くなるので、
トレードオフの関係があることに注意が必要です。
3. ホライゾン長さ T
このホライゾン長さは、
コントローラの計算能力と、
入力周期によって代わりますが、
長ければ、長いほどシステムの安定性が向上します。
シンプルなMPCの数式の導出
上記のサンプルコードではcvxpyというモデルツールを利用していますが、
モデルツールを使用せずに行列演算だけでMPCを実現したい場合は、
下記を参照下さい。
Math WorksのMPC入門ビデオ
MPCの基礎を知りたい場合は、
下記のMath Worksの入門ビデオがおすすめです。
MATLABのMPC Toolboxの説明が多いですが、
MPCの基本的な考え方もわかりやすく説明されています。
より深くモデル予測制御を学ぶために
より深くモデル予測制御を学びたい人には、
下記の本がおすすめです。

- 作者: 大塚敏之
- 出版社/メーカー: コロナ社
- 発売日: 2011/01/26
- メディア: 単行本
- 購入: 1人 クリック: 5回
- この商品を含むブログを見る

モデル予測制御―PFC(Predictive Functional Control)の原理と応用
- 作者: ジャックリシャレ,江口元,小崎恭寿男,Jacques Richalet
- 出版社/メーカー: 日本工業出版
- 発売日: 2007/02/01
- メディア: 単行本
- 購入: 1人
- この商品を含むブログを見る
入門から実際の応用まで書かれており、
非常に勉強になりました。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。

![モデル予測制御 制約のもとでの最適制御 [ ヤン・M.マチエヨフスキー ] モデル予測制御 制約のもとでの最適制御 [ ヤン・M.マチエヨフスキー ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/4605/9784501324605.jpg?_ex=128x128)