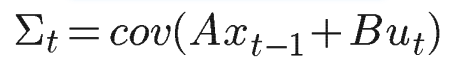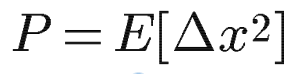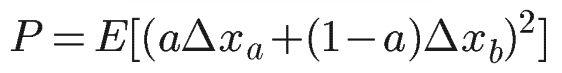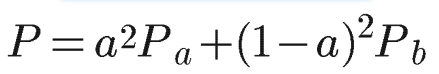目次
はじめに
移動ロボットにおいて,
自分の位置や姿勢を知ることは非常に重要です。
このように、自分の位置や姿勢をロボット自身が推定することを
自己位置推定(Localization)と呼びます。
参考: Localization (自己位置推定): 1 - MY ENIGMA
今回は,
自己位置推定の技術の一般的な方法である
拡張カルマンフィルタ(Extended Kalman Filter:EKF)の概要と、
EKFを利用した、
自己位置推定サンプルプログラム(MATLAB, Python)を紹介します。
カルマンフィルタの基礎
カルマンフィルタは、最適推定アルゴリズムの一つですが、
大きく分けて、下記の2つの用途に使用することができます。
1. 直接観測できない状態(State)を間接的な観測情報とシステムモデルから推定
2. 複数の観測値を統合して、尤もらしい状態量を推定
ロボティクスでは、
複数のセンサの情報を統合して、ロボットの位置や状態を推定したり、
センサの情報から、直接観測できないロボットの状態を推定するのに
しばしば使用されます。
カルマンフィルタの概念を学びたい場合は、
下記のYoutube動画がおすすめです。
Understanding Kalman Filters, Part 1: Why Use Kalman Filters?
Understanding Kalman Filters, Part 2: State Observers
Understanding Kalman Filters, Part 3: Optimal State Estimator
Understanding Kalman Filters, Part 4: Optimal State Estimator Algorithm
Understanding Kalman Filters, Part 5: Nonlinear State Estimators
カルマンフィルタの
アルゴリズムの導出の部分は、
下記のwikiの記事か、
下記の本を参照ください。
カルマンフィルタの応用例
カルマンフィルタの応用例としては、
下記のようなものがあります。
- 宇宙における軌跡推定・姿勢推定
- ドローンの位置姿勢推定
- 複数ロボットの協調位置推定
- 自動車のエンジンの状態量の推定
- 自動車の故障検知
- 自動車のABSにおけるタイヤと地面の相互力やタイヤ摩擦係数の推定
- 自動車の自動運転
- 電池の状態推定: 電池の残量は直接観測できないため、電池の電流と電圧でカルマンフィルタを使って推定する
- 電力配分における状態推定: 各地区における需要と供給の情報を断片的で、かつ、ノイズが含まれたデータから推定する。
EKFサンプルMATLABコード
下記がEKFサンプルコードです。
% ------------------------------------------------------------------------- % % File : ExtendedKalmanFilterLocalization.m % % Discription : Mobible robot localization sample code with % Extended Kalman Filter (EKF) % % Environment : Matlab % % Author : Atsushi Sakai % % Copyright (c): 2014 Atsushi Sakai % % License : GPL Software License Agreement % ------------------------------------------------------------------------- function [] = ExtendedKalmanFilterLocalization() close all; clear all; disp('Extended Kalman Filter (EKF) sample program start!!') time = 0; endtime = 60; % [sec] global dt; dt = 0.1; % [sec] nSteps = ceil((endtime - time)/dt); result.time=[]; result.xTrue=[]; result.xd=[]; result.xEst=[]; result.z=[]; result.PEst=[]; result.u=[]; % State Vector [x y yaw v]' xEst=[0 0 0 0]'; % True State xTrue=xEst; % Dead Reckoning xd=xTrue; % Observation vector [x y yaw v]' z=[0 0 0 0]'; % Covariance Matrix for motion Q=diag([0.1 0.1 toRadian(1) 0.05]).^2; % Covariance Matrix for observation R=diag([1.5 1.5 toRadian(3) 0.05]).^2; % Simulation parameter global Qsigma Qsigma=diag([0.1 toRadian(20)]).^2; %[v yawrate] global Rsigma Rsigma=diag([1.5 1.5 toRadian(3) 0.05]).^2;%[x y z yaw v] PEst = eye(4); tic; %movcount=0; % Main loop for i=1 : nSteps time = time + dt; % Input u=doControl(time); % Observation [z,xTrue,xd,u]=Observation(xTrue, xd, u); % ------ Kalman Filter -------- % Predict xPred = f(xEst, u); F=jacobF(xPred, u); PPred= F*PEst*F' + Q; % Update H=jacobH(xPred); y = z - h(xPred); S = H*PPred*H' + R; K = PPred*H'*inv(S); xEst = xPred + K*y; PEst = (eye(size(xEst,1)) - K*H)*PPred; % Simulation Result result.time=[result.time; time]; result.xTrue=[result.xTrue; xTrue']; result.xd=[result.xd; xd']; result.xEst=[result.xEst;xEst']; result.z=[result.z; z']; result.PEst=[result.PEst; diag(PEst)']; result.u=[result.u; u']; %Animation (remove some flames) if rem(i,5)==0 %hold off; plot(result.xTrue(:,1),result.xTrue(:,2),'.b');hold on; plot(result.z(:,1),result.z(:,2),'.g');hold on; plot(result.xd(:,1),result.xd(:,2),'.k');hold on; plot(result.xEst(:,1),result.xEst(:,2),'.r');hold on; ShowErrorEllipse(xEst,PEst); axis equal; grid on; drawnow; %movcount=movcount+1; %mov(movcount) = getframe(gcf);% アニメーションのフレームをゲットする end end toc %アニメーション保存 %movie2avi(mov,'movie.avi'); DrawGraph(result); function ShowErrorEllipse(xEst,PEst) %誤差分散円を計算し、表示する関数 Pxy=PEst(1:2,1:2);%x,yの共分散を取得 [eigvec, eigval]=eig(Pxy);%固有値と固有ベクトルの計算 %固有値の大きい方のインデックスを探す if eigval(1,1)>=eigval(2,2) bigind=1; smallind=2; else bigind=2; smallind=1; end chi=9.21;%誤差楕円のカイの二乗分布値 99% %楕円描写 t=0:10:360; a=sqrt(eigval(bigind,bigind)*chi); b=sqrt(eigval(smallind,smallind)*chi); x=[a*cosd(t); b*sind(t)]; %誤差楕円の角度を計算 angle = atan2(eigvec(bigind,2),eigvec(bigind,1)); if(angle < 0) angle = angle + 2*pi; end %誤差楕円の回転 R=[cos(angle) sin(angle); -sin(angle) cos(angle)]; x=R*x; plot(x(1,:)+xEst(1),x(2,:)+xEst(2)) function x = f(x, u) % Motion Model global dt; F = [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0]; B = [ dt*cos(x(3)) 0 dt*sin(x(3)) 0 0 dt 1 0]; x= F*x+B*u; function jF = jacobF(x, u) % Jacobian of Motion Model global dt; jF=[ 1 0 0 0 0 1 0 0 -dt*u(1)*sin(x(3)) dt*u(1)*cos(x(3)) 1 0 dt*cos(x(3)) dt*sin(x(3)) 0 1]; function z = h(x) %Observation Model H = [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ]; z=H*x; function jH = jacobH(x) %Jacobian of Observation Model jH =[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]; function u = doControl(time) %Calc Input Parameter T=10; % [sec] % [V yawrate] V=1.0; % [m/s] yawrate = 5; % [deg/s] u =[ V*(1-exp(-time/T)) toRadian(yawrate)*(1-exp(-time/T))]'; function [z, x, xd, u] = Observation(x, xd, u) %Calc Observation from noise prameter global Qsigma; global Rsigma; x=f(x, u);% Ground Truth u=u+Qsigma*randn(2,1);%add Process Noise xd=f(xd, u);% Dead Reckoning z=h(x+Rsigma*randn(4,1));%Simulate Observation function []=DrawGraph(result) %Plot Result figure(1); x=[ result.xTrue(:,1:2) result.xEst(:,1:2) result.z(:,1:2)]; set(gca, 'fontsize', 16, 'fontname', 'times'); plot(x(:,5), x(:,6),'.g','linewidth', 4); hold on; plot(x(:,1), x(:,2),'-.b','linewidth', 4); hold on; plot(x(:,3), x(:,4),'r','linewidth', 4); hold on; plot(result.xd(:,1), result.xd(:,2),'--k','linewidth', 4); hold on; title('EKF Localization Result', 'fontsize', 16, 'fontname', 'times'); xlabel('X (m)', 'fontsize', 16, 'fontname', 'times'); ylabel('Y (m)', 'fontsize', 16, 'fontname', 'times'); legend('Ground Truth','GPS','Dead Reckoning','EKF','Error Ellipse'); grid on; axis equal; function angle=Pi2Pi(angle) %ロボットの角度を-pi~piの範囲に補正する関数 angle = mod(angle, 2*pi); i = find(angle>pi); angle(i) = angle(i) - 2*pi; i = find(angle<-pi); angle(i) = angle(i) + 2*pi; function radian = toRadian(degree) % degree to radian radian = degree/180*pi; function degree = toDegree(radian) % radian to degree degree = radian/pi*180;
下記のGitHubリポジトリでも公開しています。
内容はおそらくコードを読めばわかると思いますが,
基本的には,
ホイールオドメトリとジャイロによって入力値を,
GPSとコンパスで観測値を取得し,
それらをEKFで統合しています.
このサンプルプログラムを起動すると,
自己位置推定のシミュレーションを行い,
記事冒頭のようなグラフが得られます.
このグラフを見ると分かる通り,
入力値と観測値に大きな誤差を含んでいたとしても,
高精度な位置計測ができていることがわかります.
それぞれのロボットによってセンサやモデルは異なるので
そのまま使えないことが多いと思いますが,
このコードを修正することで目的の自己位置推定ロジックを作成できるはずです.
Pythonサンプルコード
下記はPythonサンプルコードです。
""" Extended kalman filter (EKF) localization sample author: Atsushi Sakai (@Atsushi_twi) """ import numpy as np import math import matplotlib.pyplot as plt # Estimation parameter of EKF Q = np.diag([0.1, 0.1, math.radians(1.0), 1.0])**2 R = np.diag([1.0, math.radians(40.0)])**2 # Simulation parameter Qsim = np.diag([0.5, 0.5])**2 Rsim = np.diag([1.0, math.radians(30.0)])**2 DT = 0.1 # time tick [s] SIM_TIME = 50.0 # simulation time [s] show_animation = True def calc_input(): v = 1.0 # [m/s] yawrate = 0.1 # [rad/s] u = np.matrix([v, yawrate]).T return u def observation(xTrue, xd, u): xTrue = motion_model(xTrue, u) # add noise to gps x-y zx = xTrue[0, 0] + np.random.randn() * Qsim[0, 0] zy = xTrue[1, 0] + np.random.randn() * Qsim[1, 1] z = np.matrix([zx, zy]) # add noise to input ud1 = u[0, 0] + np.random.randn() * Rsim[0, 0] ud2 = u[1, 0] + np.random.randn() * Rsim[1, 1] ud = np.matrix([ud1, ud2]).T xd = motion_model(xd, ud) return xTrue, z, xd, ud def motion_model(x, u): F = np.matrix([[1.0, 0, 0, 0], [0, 1.0, 0, 0], [0, 0, 1.0, 0], [0, 0, 0, 0]]) B = np.matrix([[DT * math.cos(x[2, 0]), 0], [DT * math.sin(x[2, 0]), 0], [0.0, DT], [1.0, 0.0]]) x = F * x + B * u return x def observation_model(x): # Observation Model H = np.matrix([ [1, 0, 0, 0], [0, 1, 0, 0] ]) z = H * x return z def jacobF(x, u): """ Jacobian of Motion Model motion model x_{t+1} = x_t+v*dt*cos(yaw) y_{t+1} = y_t+v*dt*sin(yaw) yaw_{t+1} = yaw_t+omega*dt v_{t+1} = v{t} so dx/dyaw = -v*dt*sin(yaw) dx/dv = dt*cos(yaw) dy/dyaw = v*dt*cos(yaw) dy/dv = dt*sin(yaw) """ yaw = x[2, 0] v = u[0, 0] jF = np.matrix([ [1.0, 0.0, -DT * v * math.sin(yaw), DT * math.cos(yaw)], [0.0, 1.0, DT * v * math.cos(yaw), DT * math.sin(yaw)], [0.0, 0.0, 1.0, 0.0], [0.0, 0.0, 0.0, 1.0]]) return jF def jacobH(x): # Jacobian of Observation Model jH = np.matrix([ [1, 0, 0, 0], [0, 1, 0, 0] ]) return jH def ekf_estimation(xEst, PEst, z, u): # Predict xPred = motion_model(xEst, u) jF = jacobF(xPred, u) PPred = jF * PEst * jF.T + Q # Update jH = jacobH(xPred) zPred = observation_model(xPred) y = z.T - zPred S = jH * PPred * jH.T + R K = PPred * jH.T * np.linalg.inv(S) xEst = xPred + K * y PEst = (np.eye(len(xEst)) - K * jH) * PPred return xEst, PEst def plot_covariance_ellipse(xEst, PEst): Pxy = PEst[0:2, 0:2] eigval, eigvec = np.linalg.eig(Pxy) if eigval[0] >= eigval[1]: bigind = 0 smallind = 1 else: bigind = 1 smallind = 0 t = np.arange(0, 2 * math.pi + 0.1, 0.1) a = math.sqrt(eigval[bigind]) b = math.sqrt(eigval[smallind]) x = [a * math.cos(it) for it in t] y = [b * math.sin(it) for it in t] angle = math.atan2(eigvec[bigind, 1], eigvec[bigind, 0]) R = np.matrix([[math.cos(angle), math.sin(angle)], [-math.sin(angle), math.cos(angle)]]) fx = R * np.matrix([x, y]) px = np.array(fx[0, :] + xEst[0, 0]).flatten() py = np.array(fx[1, :] + xEst[1, 0]).flatten() plt.plot(px, py, "--r") def main(): print(__file__ + " start!!") time = 0.0 # State Vector [x y yaw v]' xEst = np.matrix(np.zeros((4, 1))) xTrue = np.matrix(np.zeros((4, 1))) PEst = np.eye(4) xDR = np.matrix(np.zeros((4, 1))) # Dead reckoning # history hxEst = xEst hxTrue = xTrue hxDR = xTrue hz = np.zeros((1, 2)) while SIM_TIME >= time: time += DT u = calc_input() xTrue, z, xDR, ud = observation(xTrue, xDR, u) xEst, PEst = ekf_estimation(xEst, PEst, z, ud) # store data history hxEst = np.hstack((hxEst, xEst)) hxDR = np.hstack((hxDR, xDR)) hxTrue = np.hstack((hxTrue, xTrue)) hz = np.vstack((hz, z)) if show_animation: plt.cla() plt.plot(hz[:, 0], hz[:, 1], ".g") plt.plot(np.array(hxTrue[0, :]).flatten(), np.array(hxTrue[1, :]).flatten(), "-b") plt.plot(np.array(hxDR[0, :]).flatten(), np.array(hxDR[1, :]).flatten(), "-k") plt.plot(np.array(hxEst[0, :]).flatten(), np.array(hxEst[1, :]).flatten(), "-r") plot_covariance_ellipse(xEst, PEst) plt.axis("equal") plt.grid(True) plt.pause(0.001) if __name__ == '__main__': main()
下記のGitHubリポジトリでも公開しています。
共分散行列の更新において、なぜヤコビ行列で挟むのか?
上記のEKFのアルゴリズムにおいて、
前から不思議に思っていたのが、
「共分散行列の更新において、なぜヤコビ行列で挟むのか?」
ということです。
上記のプログラムでいうところの、
Predictにおける共分散の更新である
PPred= F*PEst*F' + Q;
の部分や、
Updateにおける共分散の更新である
S = H*PPred*H' + R;
のことです。
基本的には、時系列的に一つ前の共分散行列を
ヤコビ行列とその転置行列で挟んで、誤差共分散行列を足しています。
これまで、何故こんなことをしているのかがわかっていませんでした。
今回、少し調べてみたらなんとなく理解することができたので、
メモとして残しておきます。
まず初めに、下記のような基本的な線形モデルを考えます。
MATLABプログラムにおける, Motion ModelやObservation Modelのことですね。
ここで、時刻t-1の時の共分散行列 Σt-1から,
時刻tの時の共分散行列Σtを計算してみたいと思います。
まず初めに、時刻tの共分散行列Σtは, 時刻tの時のx_tの共分散の値なので
となります。
ここでcovは下記のwikiのページにあるように、
ある状態ベクトルの共分散を表します。
続いて、先ほどの線形システムの式を代入すると、
となります。
ここで、先ほどのwikiの性質5を使用すると、
のように、2つの共分散行列にわけることができます。
続いて、
一つ目の項は、先ほどのwikiの性質7のA=Bの時のことを考えると、
となり、
二つ目の項は、自分のカルマンフィルタにおいては
入力による共分散を、誤差共分散Rと定義しているため、
先ほどの式は、
となります。
すると、cov(x_t-1)は、時刻t-1の時の共分散行列になるので、
となり、カルマンフィルタの式とほぼ同じ式が導出できました。
最後に、
一般的にロボティクスのモデルは、
最初に定義した線形モデルではなく非線形モデルです。
これまでの式の展開は、モデルが線形でなければ成り立ちません。
そこで、ヤコビ行列を使ってモデルを線形化したのが、
拡張カルマンフィルタなのです。
すると先ほどの式のAを、近似されたヤコビ行列Jで置き換えると
となり、目的の式を導出できました。
これが共分散行列を更新する時にヤコビ行列で挟む理由になります。
自分的にはかなりすっきりしました。
カルマンフィルタを身近に感じるために
前述のサンプルコードのようにアルゴリズムを実装すれば
カルマンフィルタを実装することはそこまで難しくはありません。
しかし、カルマンフィルタが実際にどのように機能しているのかを
イメージとして捉えるのは多少難しいと思います。
そこで、非常に簡単な例題を元に、
カルマンフィルタの考え方を説明したいと思います。
カルマンフィルタは一言で言ってしまうと
"2つの確率の重み付き足し算の結果の
誤差(分散)が最小になるように、重みを計算する"
方法であると言えます。
ロボティクスの自己位置推定においては、
デットレコニングの位置情報と、
GPSの位置情報を組み合わせて、
最終的な位置情報の誤差が最小になるように、
それぞれの位置情報の重みを逐次的に計算してるのです。
では、単純な例題でカルマンフィルタの式を導出したいと思います。
まず初めに一次元の2つのガウス分布の状態量(平均x,分散P)
x_a, P_aとx_b, P_bを考えます。
これら2つをどのようにカルマンフィルタは統合するのでしょうか。
ちなみにこの2つのガウス分布は独立であるとします。
カルマンフィルタでは下記のような重み付き線形結合を使用して、
2つの確率を統合します。
ここでxは統合後の平均値であり、
aはx_aの重みです。
重みはすべて足すと1になることを考えると、
x_bの重みは1-aとなります。
カルマンフィルタはこのaの値を
xの分散Pの値が最小になるように決定しているのです。
では、分散Pを最小にするようにaを決めるとは、
どのようにするのでしょうか?
まず初めに分散Pは分散の定義そのものから、
となります。
ここでEは期待値を表しており、Δxは平均値からの差を表しています。
すると、この式に先ほどの式(i)を代入すると
となり、これを展開して整理すると、
となります。
ここで前述の通り、aとbは独立なので、
E[Δx_aΔx_b]=0となり、分散の定義をより
E[Δx_a^2]=P_a, E[Δx_b^2]=P_bなので、
となります。
続いて、このPを最小化するaを求めてみましょう。
よくやる方法ですが、
最小値はPをaで微分した値が0である時だと考えます。
つまり、
となり、これをaで整理すると、
となります。
よって、Pを最小化するaの値が決まったので、
これを式(i)に代入すると、
となります。
ここで、この式をじっくりと見てみると、P_aとP_bの値の大きさから
きちんと重み付け足し算をしていることがわかります。
例えば、P_aの値がP_bの値よりも大きかった場合、
x_aにかかる重みは相対的に小さくなり、
最終的な正規分布に対する寄与度が小さくなります。
その分x_bの寄与度は大きくなるのです。
つまり、誤差(分散)が小さいものを信用して、
大きいものを無視するように、確率が計算されるのです。
そして、この式を意図的に変形させると下記のようにできます。
すると、この式が何か見覚えのある式に見えてこないでしょうか?
そうです, x_bを観測値、x_aを入力による更新値と考えると、
x_b-x_aはイノベーション(サンプルコードにおけるy)を表しており、
その前の分数の部分をカルマンゲインKと置くと、
先ほどの式は、まさにカルマンフィルタにおける平均値の更新になるのです。
ちなみに、分散値Pも同じように式(ii)にaを代入すると、
となり、これを再び意図的に変形させると(笑)
となり、先ほどと同様に分数の部分をKと置くと、
カルマンフィルタにおける共分散行列の更新の式にほぼ一致するのです。
(実際はモデルによる遷移があるため、ヤコビ行列などが入ってきて少し形は変わりますが。。。)
以上のように、
カルマンフィルタは、ベースは分散最小とするような重み付き足し算であり、
上記の方法で、カルマンフィルタ(っぽいもの)は導出できるのです。
少しカルマンフィルタが身近に感じられたのは自分だけでしょうか?(笑)
その他のロボティクスアルゴリズムのサンプルコードや関連資料
こちらを参照下さい。
また、ロボティクスに関連する資料は下記を参照下さい。