目次
- 目次
- はじめに
- 行列
- 行列演算の応用例
- 線形変換
- 線形動的モデル
- 行列の掛け算
- 逆行列
- 線形方程式の解法
- なぜ線形方程式を解くのに、逆行列を使ってはいけないのか？
- Pseudo inverse 疑似逆行列
- 参考資料
- MyEnigma Supporters
はじめに
スタンフォード大学には
機械学習を学ぶ上での第一歩として、
Introduction to Matrix Methods (EE103)という授業があります。
今回の記事では、
この授業の教科書である
Introduction to Applied Linear Algebraを
読んだ際の技術メモです。
この教科書は下記のリンクのページから
pdfをダウンロードすることができます。
本記事では、
上記の教科書の行列の部分のみのメモです。
他の部分に関しては、下記の記事を参照下さい。
行列
行列の基礎
行列のインデックスも、
ベクトルと同じようにプログラミング言語によって、
インデックスの表し方が異なる。
多くの低レベルプログラミング言語では、
行列のインデックスは０始まりだが、
幾つかの高レベル言語では、
1始まりの場合もある。
多くの教科書や論文では、
行列は大文字のアルファベットで表し(例:A)
ベクトルは小文字のアルファベットで表す（例:a)
行列データの例
画像
降水量データ (m個の場所におけるn時間の降水量データ)
投資回収 (m個のアセットにおけるn期間の利益率)
疎行列
nnz(A)はAの各要素の０でない要素の数を表し、
nnz(A)が小さい行列を疎行列という。
疎行列は効率的に保存する方法があり、
多くのデータ(購入行列など)は大抵疎行列である。
三角行列は50%は0でないため、スパースではない。
転置
行列の転置は、部分行列の場所を転置し、
その部分行列を転置したものと同じになる。
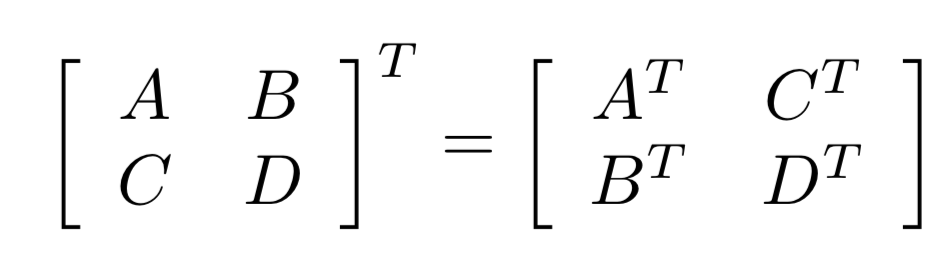
行列ノルム
行列のノルムの代表的なものに、
フロベニウスノルムがあり、
||A||_F や ||A||と表記される。
フロベニウスノルムは、行列の各要素の二乗の総和のルートである。
行列のノルムは、行列の各ベクトルのノルムの和と同じになる。
行列の掛け算
ベクトルに行列を掛け算することにより、
べクトルの差分を計算することができる。
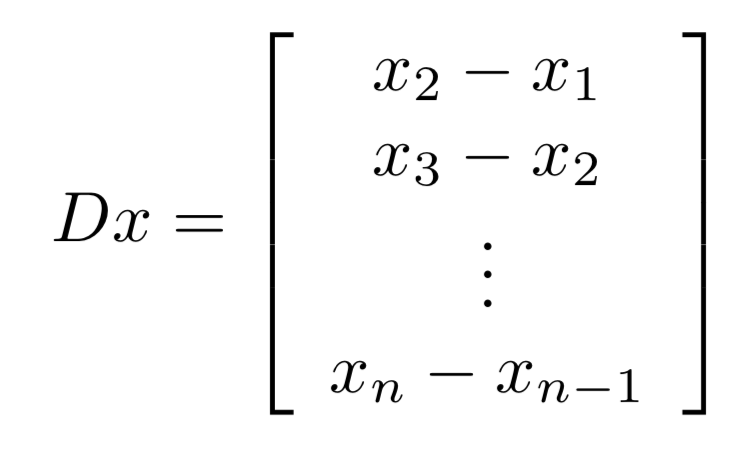
また、同じように
ベクトルの累積和ベクトルを計算することもできる。
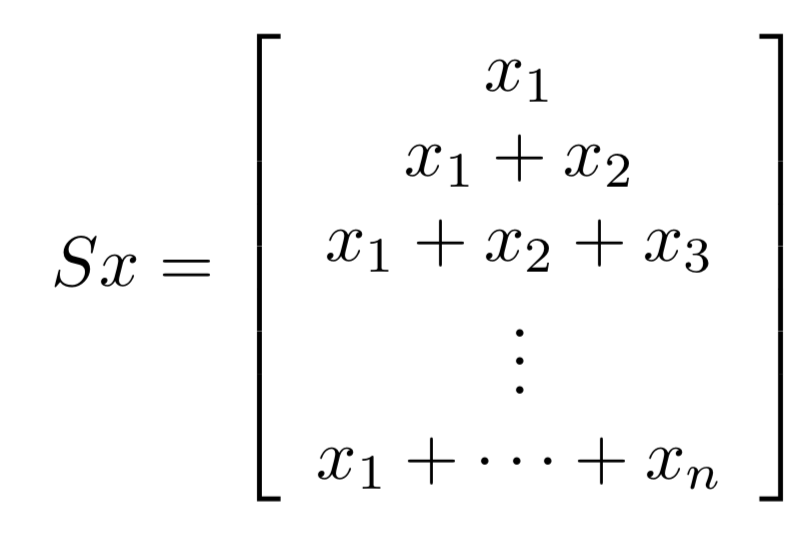
行列演算の応用例
幾何学的変換
スケール変換
回転
同次変換
セレクター (ベクトルの一部を抽出したり、順番を変える)
画像のダウンサンプリング
グラフ構造
ネットワーク
畳み込み
畳み込みの計算は*(アスタリスク)で表すことができ、
行列の掛け算で表すことができる。
mean filter、画像のぼかしフィルターなどは
Convolutionで表すことができる。
この畳込みｎ計算は、高速に計算するアルゴリズムがあり、
Fast FFTなどで利用されている。
線形変換
多くの関数は、
線形 y = Axやアフィンy = Ax+bに近似することで、
利用しやすくなる。
その近似手法の一つがテイラー展開である。
線形動的モデル
下記の式を線形動的モデルと呼ぶ。
線形動的モデルでは、
Aが時刻によって変わらないAt=At-1のことを、
Time invariant モデルといい、
ut(input)とct(offset)はシステム外部からの、
システムへの影響を表す。
この線形動的モデルのように、
次の状態が現在の状態のみに依存することを
マルコフ性という。
この線形動的モデルを利用することにより、
各年齢の人口分布の推移
伝染病のモデル
物体の運動
需要と供給のモデル
などを表すことができる。
行列の掛け算
ベクトルの内積: a^Tb
ベクトルの外積: ab^T
ある行列Aに対して、
G = A^TAとなる行列をグラム行列という。
ある行列Qにおいて、転置した行列と
逆行列が同じ行列を直交行列という。
Q^T = Q^-1
QR分解とは、
ある行列Aを、ある直交行列Qと、
上三角行列Rに分解すること。
A = QR
このQR分解をすることにより、
ある行列の逆行列が計算できるようになる。
QR分解の代表的なアルゴリズムとして、
グラム・シュミッドアルゴリズムがある。
逆行列
ある正方行列の逆行列を計算できる場合、
その行列を可逆行列 invertible matrixと言う。
一方、逆行列を計算できない行列を、
特異行列singular matrixという。
ある行列がsingular matrixであるかどうかは、
行列のrankが行列の行や列のサイズより小さい(ランク落ち)
行列式が0
などで判断できる。
線形方程式の解法
上三角行列Rに対して、
Rx =b
という形の線形方程式は、
Back substitution(後退代入法)を使うことで解くことができる。
通常の行列Aに対して、
Ax = b
という線形方程式を解く場合は、
まず初めに、AをQR分解し、
A = QRを計算し、
QRx = bから、
Qは直行行列であるため、
両辺の左からQ^-1を掛けて、
Q^-1QRx = Q^-1bより、
Rx = Q^-1b = Q^T bとなる。
あとは、QR分解の結果のRとQを使って、
上記の上三角行列の線形方程式を
Back substitutionで解けば、
逆行列が計算できる。
逆行列の計算量は行列の次元をnとすると、
約3n^3である。
Ax = bの式において、A^-1bを計算する演算を
バックスラッシュで表すプログラミング言語もある。
(MATLABなど)
この逆行列を利用することにより、
多項式補間
化学反応の平衡シミュレーション
熱放射シミュレーション
などを実施することができる。
なぜ線形方程式を解くのに、逆行列を使ってはいけないのか？
しばしば、MATLABでは、線形方程式を解くのに、
逆行列を計算するinv()関数を使わずに、専用の演算子であるバックスラッシュを使うことが推奨されています。
これは、inv()関数の実装にもよるのですが、一般的に線形方程式は、
QR分解とback substitutionを使うことで、
逆行列を計算せずに効率的に計算することが可能です。
逆行列を計算する場合はnxnの行列のメモリのアロケーションも発生するため、
一般的に計算負荷が大きいと言われています。
参考:
Pseudo inverse 疑似逆行列
over determinedやunder-determinedな線形方程式における
逆行列は疑似逆行列として計算できる。
疑似逆行列の計算としては、
A = QRのQR分解が計算出来た場合、
疑似逆行列 A^+は、
A^+ = R^-1 Q^T
で計算でき、
A^T = QRのQR分解が計算出来た場合は、
A^+ = Q (R^-1)^T
で計算できる。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
