目次
- 目次
- はじめに
- グリッドマップのデータ表現方法
- Grid Mapシミュレーション1: End Point Update
- 1. 観測点をグローバル座標系に変換する
- 2. グローバル座標系の観測点の位置をグリッドマップ座標系に変換する
- 3. x-y方向それぞれのグリッドインデックスを計算する
- 4. 一次元配列のデータ配列のインデックスを計算する
- 5. 一次元配列のデータの更新
- Grid Mapシミュレーション2: Gaussian Likelihood Update
- Grid Mapシミュレーション3: Ray Casting Update
- 時系列データによる占有度の計算
- Grid Mapに格納するデータ
- Grid Mapを利用する利点
- MATLABサンプルコード
- Pythonサンプルコード
- グリッドマップに関して、より詳しく学びたい方は
- その他自律移動技術を学びたい方は
- 参考資料
- MyEnigma Supporters
はじめに
自律移動ロボットにとって、
空間を格子状に区切った
格子地図(Grid Map)は、
非常に重要な地図構築技術です。
一般的なパスプランニングアルゴリズムである、
ダイクストラ法やA*は、
Grid Mapで作成した地図であれば、
そのまま応用可能です。
また、地図と自己位置を同時に推定する
Simultaneous Localization And Mapping:SLAMにおいて、
(SLAM技術に関しては下記を参照下さい
地図として、Grid Mapがよく使用されます。
しかし、自分はこれまで
Grid Mapを使用した論文を
色々読んできましたが、
実際にグリッドマップを使用する時の
データの取り扱いや探索方法を
わかりやすく説明した資料には
出会うことができませんでした。
仕方が無いので、自分はこれまで、
グリッドマップを使用した
オープンソースのコードをなどを見て、
コツコツとグリッドマップの使い方を勉強してきたのですが、
最近やっと、実際のロボットでも
このグリッドマップを使用できるようになってきました。
今回、折角勉強したので、
これまで学んできたGrid Mapの技術内容と、
それらの技術を利用した、
MATLAB, Pythonサンプルプログラムを公開したいと思います。
グリッドマップのデータ表現方法
まず初めに、
これから説明するグリッドマップの
MATLABシミュレーションで
使用しているグリッドマップのデータの
表現方法について説明します。
基本的にはROSのnav_msgs::OccupacyGridと
nav_msgs/OccupancyGrid Documentation
同じデータ構成です。
まず初めにグリッドマップの設定情報として、
下記の5種類のデータを有しています。
1. W (Width): x方向(横方向)のグリッド数
2. H (Height): y方向(縦方向)のグリッド数
3. R (Resolution): 一つの正方形グリッドの一辺の長さ[m]
4. C_x (Center X): グリッドの中心のx座標[m]
5. C_y (Center Y): グリッドの中心のy座標[m]
基本的にこれらのデータは
グリッドマップを作成した最初に設定した後は変更しません。
しかし、ロボット中心のグリッドマップを作成する場合は、
CXとCYはロボットが移動するにつれて、変化することになります。
続いて、各グリッドに格納されるデータは
6. Data[W*H]: 各グリッドの中に格納されたデータの一次元配列(ベクトル)
となります。
このグリッドマップのグリッドの総数はW*Hで計算できます。
基本的なグリッドマップは上記の6種類のデータで構成されます。
Grid Mapシミュレーション1: End Point Update
まず初めにEnd Point Updateという
最も一般的なグリッドマップの更新方法を
説明したいと思います。
End Point Updateは、
ある観測点の位置に対応するグリッドの
データを更新することです。
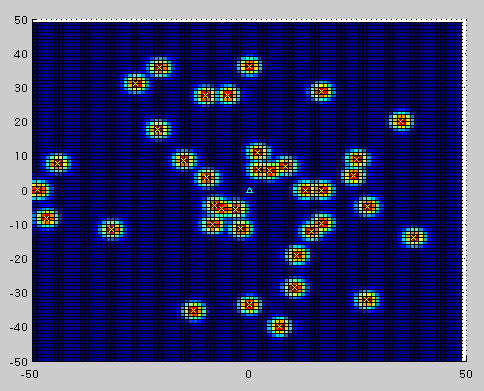
上記の図では、
ある複数の観測点(黄色いバツ)が与えられた時、
それに対応するグリッドの占有データを
増加させた場合のシミュレーション結果です。
点が格納されていない所は青ですが、
格納された場所は赤色になっていることがわかります。
(青 -> 赤 := データの数値 小 -> 大)
End Point Updateは下記の流れで実施します。
1. 観測点をグローバル座標系に変換する
同次変換を使用して、ロボットの位置姿勢(x,y,yaw)から、
ロボット座標系での観測点をグローバル座標に変換します。
今回のMALTABプログラムでは、
すでにグローバル座標系の位置が取得できていることを仮定しています。
2. グローバル座標系の観測点の位置をグリッドマップ座標系に変換する
グリッドマップがグローバル座標系のx-yと方位が同じ場合、
下記の式のように、グリッドマップの中心値から引けば
グリッドマップ座標系に変換できます。
もし、グローバル座標系とグリッド座標系の
角度が違う場合は、
先ほどと同様に同時変換をもう一度しましょう。
3. x-y方向それぞれのグリッドインデックスを計算する
続いて、距離情報であるグリッド座標系のx-y値を
それぞれのx-y方向のグリッドのx-yインデックス値に変換します。
つまり、ある観測値が格納されるグリッドの
x方向とy方向のインデックスを計算するということです。
下記の式のように、グリッドマップの設定値を使用すると
簡単にグリッドのx-yインデックスを計算することができます。
ここで、i_x,i_yはグリッドマップのx-y方向のそれぞれのインデックス値であり、
floorは床関数を表しています。(つまり小数点切り捨てて、整数値にしている)
床関数を使用するのは、インデックスは整数値であり、
この切り捨て部分がグリッドマップにおける量子化に相当します。
C++の場合は、この床関数はintでキャストすれば良いでしょう。
ちなみに、W/2やH/2で引いているのは、
グリッドマップの中心の座標系から、
グリッドマップの左下座標系に変換しているからです。
(最終的なグリッドマップのデータは、一番左下のグリッドが
インデックス0 [MATLABの場合は1]になる)
また、この時点でそれぞれのx-yインデックスが、
グリッドマップのサイズ(W,H)を超えていないかを
確認したほうが良いと思います。
ちなみに、グリッドマップの下限(左下)の座標をl_x, l_yとした場合は、
下記のよりシンプルな式でグリッドのインデックスを計算することができます。
4. 一次元配列のデータ配列のインデックスを計算する
続いて、先ほどのx-y方向のグリッドインデックス値から、
最終的なデータが格納されている一次元配列のインデックスを計算します。
一次元配列のインデックスiは下記の式で簡単に計算できます。
または、
以上の式において、どちらを使用するかは、
一次元配列のデータ格納を
[x1, y1] [x1, y2], [x1, y3] .... [x1, yN], [x2, y1] ...
のように、まず初めにあるxの値を基準として、
すべてのyのグリッドを並べるか、
[x1, y1] [x2, y1], [x3, y1] .... [xN, y1], [x1, y2] ...
のようにその逆かによって変わります。
5. 一次元配列のデータの更新
先ほど計算されたインデックスの値が、
対応するグリッドなので、そのデータを更新します。
今回のMATLABシミュレータの場合は、
すべてのグリッドを0.5(Unknown)で初期化し、
対応するグリッドの値を下記の式のように1.0と更新しました。
以上で、最も単純なEnd Point Updateは完了です。
Grid Mapシミュレーション2: Gaussian Likelihood Update
続いて、Gaussian Likelihood Updateについて説明します。
これはそれぞれの観測値に近ければ近いほど、
グリッドの値を高くするようなUpdateの方法です。
観測値の近くかどうかを、
ガウス分布を使用して評価することにより
上記の図のように、観測点に近ければ近いほど
グリッドの値が大きくなる(赤色)に更新することができます。
このようなグリッドマップは尤度場(Likelihood field)と呼ばれ、
Scanデータによる位置計測であるモンテカルロ位置計測や、
できるだけ障害物に近づかないようなパスを生成する、
ポテンシャルフィールドにも使用されます。
このGaussian Likelihood Updateは、
大きく分けて2つ計算する方法があります。
一つ目は、
すべてのグリッドマップのグリッドを
1つづつ選択し、そのグリッドから
最近傍の観測点までの距離を計算し、
その距離をガウス分布に当てはめて尤度を計算する方法です。
二つ目は、それぞれの観測値に対し、
その観測値が格納されたグリットの近傍グリッドを計算して、
その近傍グリッドとの距離をガウス分布に当てはめて
尤度を計算する方法です。
基本的にはどちらでも計算可能ですが、
全体のグリッドの数に対して、観測点が少ない場合、
二つ目の方法の方が計算が早くなります。
今回のMATLABシミュレータでは、
一つ目のすべてのグリッドを探索する方法を用いています。
先ほどのEnd Point Updateと逆に、
一次元配列のあるグリッドインデックスから、
そのグリッドの中心点のグローバル座標を計算する必要がありますが、
これは基本的にEnd Point Updateで行った計算の逆を実施すればOKです。
(基本的に簡単な1次関数なので、逆関数を計算するのは簡単です)
そして、それぞれのグリッドのx-y座標から、
すべての観測点までのノルム距離を計算し、
その値の最小値と、ガウス分布を使用して、
そのグリッドに格納される尤度を計算しています。
下記はPythonサンプルコードです。
""" 2D gaussian grid map sample author: Atsushi Sakai (@Atsushi_twi) """ import math import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm EXTEND_AREA = 10.0 # [m] grid map extention length show_animation = True def generate_gaussian_grid_map(ox, oy, xyreso, std): minx, miny, maxx, maxy, xw, yw = calc_grid_map_config(ox, oy, xyreso) gmap = [[0.0 for i in range(yw)] for i in range(xw)] for ix in range(xw): for iy in range(yw): x = ix * xyreso + minx y = iy * xyreso + miny # Search minimum distance mindis = float("inf") for (iox, ioy) in zip(ox, oy): d = math.sqrt((iox - x)**2 + (ioy - y)**2) if mindis >= d: mindis = d pdf = (1.0 - norm.cdf(mindis, 0.0, std)) gmap[ix][iy] = pdf return gmap, minx, maxx, miny, maxy def calc_grid_map_config(ox, oy, xyreso): minx = round(min(ox) - EXTEND_AREA / 2.0) miny = round(min(oy) - EXTEND_AREA / 2.0) maxx = round(max(ox) + EXTEND_AREA / 2.0) maxy = round(max(oy) + EXTEND_AREA / 2.0) xw = int(round((maxx - minx) / xyreso)) yw = int(round((maxy - miny) / xyreso)) return minx, miny, maxx, maxy, xw, yw def draw_heatmap(data, minx, maxx, miny, maxy, xyreso): x, y = np.mgrid[slice(minx - xyreso / 2.0, maxx + xyreso / 2.0, xyreso), slice(miny - xyreso / 2.0, maxy + xyreso / 2.0, xyreso)] plt.pcolor(x, y, data, vmax=1.0, cmap=plt.cm.Blues) plt.axis("equal") def main(): print(__file__ + " start!!") xyreso = 0.5 # xy grid resolution STD = 5.0 # standard diviation for gaussian distribution for i in range(5): ox = (np.random.rand(4) - 0.5) * 10.0 oy = (np.random.rand(4) - 0.5) * 10.0 gmap, minx, maxx, miny, maxy = generate_gaussian_grid_map( ox, oy, xyreso, STD) if show_animation: plt.cla() draw_heatmap(gmap, minx, maxx, miny, maxy, xyreso) plt.plot(ox, oy, "xr") plt.plot(0.0, 0.0, "ob") plt.pause(1.0) if __name__ == '__main__': main()
このコードを実行すると、下記のようなシミュレーションが表示されます。
Grid Mapシミュレーション3: Ray Casting Update
最後のシミュレーションがキャスティングと呼ばれる
グリッドマップのアップデート方法です。
これは距離センサ特有の特徴である、
オクルージョン(物体遮蔽)を考慮したグリッドマップ更新方法です。
アンビエントオクルージョン・はじめの一歩 - アンビエントオクルージョンちゃん
どこに障害物がいるかをグリッドマップで表現する場合には、
上記の2つの更新方法でも良いのですが、
1.観測した上で、安全
2.観測した上で、危険
3.観測していない
といったような評価をしたい場合には、
上記の更新方法では難しいです。
本当に安全にロボットが走行するためには、
観測して上で、安全なのかどうかを
判断することが重要になります。
(障害物によって遮蔽されて、
安全確認できなかった場所は走行すべきではない)
距離計測センサは、センサの中心から
ある角度毎にビーム状の探索を行い、
周辺の障害物までの距離を計算していると考えることができます。
つまり、
センサ中心から、観測値が得られた直前までが、安全な場所であり、
観測値が得られた場所は、危険であり、
それより先は、まだ観測していないと判断できます。
これを実現したのがレイキャスティングです。
レイキャスティイング更新を行うことにより、
上記のシミュレーション結果のように、
観測点の付近まではFree (グリッドの値→0:青)になり、
観測点の場所はOccupied(グリッド値→1:赤)になり、
それより先はUnknown(グリッド値=0.5:緑)の初期値のまま
になります。
一般的な自律移動ロボットの地図構築では、
このレイキャスティング更新で作成された地図を使用します。
なぜなら、観測した上で安全だと判定された領域のみを用いて、
ナビゲーションをすることが可能であり、
非常に安全な自律移動が可能になるからです。
また、先ほど説明したモンテカルロ位置計測においても、
このレイキャスティング更新を利用することがあります。
これは前述の2つの更新方法とは異なり、
障害物がある場所の情報(Occupoed)だけでなく、
障害物がない場所の情報(Free)も使って
位置計測をすることができるからです。
このレイキャスティングを利用する際に
一つ問題になるのが計算コストです。
レイキャスティング更新を実現する上で、
一番簡単な方法は、それぞれの観測点に対して、
すべてのグリッドを計算して、
ビームの幅から対応するグリッドを探索し、
それらのグリッドをセンサ中心からの距離で識別して、
グリッドを更新するという方法です。
しかし、これは非常に計算コストが大きいです。
これを解決する方法がプレキャスティングです。
これは、センサの角度解像度とグリッドマップの設定は、
地図作成時から変わることが無いということを利用したものです。
事前にすべてのグリッドを探索して、
各角度解像度毎のビンの対応するグリッドのインデックスを
センサ中心からの距離でソートしておいた状態で
データベースに追加しておき、
それを使ってグリッドを毎回探索することなく、
グリッドを更新する方法です。
具体的には、ある観測値を得られた時、
その角度値からプレキャスティングモデルのビンを選択し、
そのビン内のグリッドに対して、
事前に計算した距離情報から、観測点より
近いグリッドと、同じ距離のグリッド、そして遠いグリッドを
選択するため、非常に計算コストを低く抑えることができます。
おそらく具体的な方法に関しては、
MATLABのサンプルコードのPrecasting関数を見てもらったほうが
わかりやすいかと思います。
下記はRaycastingのPythonサンプルコードです。
""" Ray casting 2D grid map example author: Atsushi Sakai (@Atsushi_twi) """ import math import numpy as np import matplotlib.pyplot as plt EXTEND_AREA = 10.0 show_animation = True def calc_grid_map_config(ox, oy, xyreso): minx = round(min(ox) - EXTEND_AREA / 2.0) miny = round(min(oy) - EXTEND_AREA / 2.0) maxx = round(max(ox) + EXTEND_AREA / 2.0) maxy = round(max(oy) + EXTEND_AREA / 2.0) xw = int(round((maxx - minx) / xyreso)) yw = int(round((maxy - miny) / xyreso)) return minx, miny, maxx, maxy, xw, yw class precastDB: def __init__(self): self.px = 0.0 self.py = 0.0 self.d = 0.0 self.angle = 0.0 self.ix = 0 self.iy = 0 def __str__(self): return str(self.px) + "," + str(self.py) + "," + str(self.d) + "," + str(self.angle) def atan_zero_to_twopi(y, x): angle = math.atan2(y, x) if angle < 0.0: angle += math.pi * 2.0 return angle def precasting(minx, miny, xw, yw, xyreso, yawreso): precast = [[] for i in range(int(round((math.pi * 2.0) / yawreso)) + 1)] for ix in range(xw): for iy in range(yw): px = ix * xyreso + minx py = iy * xyreso + miny d = math.sqrt(px**2 + py**2) angle = atan_zero_to_twopi(py, px) angleid = int(math.floor(angle / yawreso)) pc = precastDB() pc.px = px pc.py = py pc.d = d pc.ix = ix pc.iy = iy pc.angle = angle precast[angleid].append(pc) return precast def generate_ray_casting_grid_map(ox, oy, xyreso, yawreso): minx, miny, maxx, maxy, xw, yw = calc_grid_map_config(ox, oy, xyreso) pmap = [[0.0 for i in range(yw)] for i in range(xw)] precast = precasting(minx, miny, xw, yw, xyreso, yawreso) for (x, y) in zip(ox, oy): d = math.sqrt(x**2 + y**2) angle = atan_zero_to_twopi(y, x) angleid = int(math.floor(angle / yawreso)) gridlist = precast[angleid] ix = int(round((x - minx) / xyreso)) iy = int(round((y - miny) / xyreso)) for grid in gridlist: if grid.d > d: pmap[grid.ix][grid.iy] = 0.5 pmap[ix][iy] = 1.0 return pmap, minx, maxx, miny, maxy, xyreso def draw_heatmap(data, minx, maxx, miny, maxy, xyreso): x, y = np.mgrid[slice(minx - xyreso / 2.0, maxx + xyreso / 2.0, xyreso), slice(miny - xyreso / 2.0, maxy + xyreso / 2.0, xyreso)] plt.pcolor(x, y, data, vmax=1.0, cmap=plt.cm.Blues) plt.axis("equal") def main(): print(__file__ + " start!!") xyreso = 0.25 # x-y grid resolution [m] yawreso = np.deg2rad(10.0) # yaw angle resolution [rad] for i in range(5): ox = (np.random.rand(4) - 0.5) * 10.0 oy = (np.random.rand(4) - 0.5) * 10.0 pmap, minx, maxx, miny, maxy, xyreso = generate_ray_casting_grid_map( ox, oy, xyreso, yawreso) if show_animation: plt.cla() draw_heatmap(pmap, minx, maxx, miny, maxy, xyreso) plt.plot(ox, oy, "xr") plt.plot(0.0, 0.0, "ob") plt.pause(1.0) if __name__ == '__main__': main()
実行すると下記のようなシミュレーションが表示されます。
時系列データによる占有度の計算
上記の例は、一回の観測によって
グリッドマップの占有度(物体の有無)
を判断しています。
しかし、実際はセンサに観測値にもノイズが含まれるため
一度の観測値のみで判断するのではなく、
複数回の観測値を考慮した上で、
物体の有無を判断します。
具体的には、それぞれのグリッドマップに
物体の有無を表す占有確率(Occupancy)を連続値の値として保持しておき
その占有確率をセンサの観測値と事前のセンサのノイズ量を踏まえて
ベイズ理論を使って確率を更新するようにします。
これによりセンサのデータを取得する度に、
占有確率を更新することができ、
時間が経てば立つほど、正しい地図を生成することができます。
ベイズ理論に関しては、下記の資料を参照下さい。
また実際には、占有確率の計算コスト削減と
占有確率計算の安定性向上のために
対数オッズという値で占有確率を表現する方法が良く使われるようです。
対数オッズに関しては下記の資料を参照下さい
Grid Mapに格納するデータ
Grid Mapに格納するデータとしては、
前述した、周辺環境における障害物の有無の確率を格納した
占有格子地図(Occupancy Grid Map:OGM)が一番ポピュラーですが、
それ以外にもデータを格納できます。
例えば、そのグリッドに存在する物体の高さを格納した
Hight Map (Digital Elevation Map:DEMとも呼ばれる)は、
地形の3D形状を表現するのに、手軽であるため
しばしば使用されるようです。
また、グリッドに存在する物体の色や反射強度を格納することも可能です。
例えば、道路の白線を認識するために、
道路面をグリッドマップで区切り、
その中にセンサからの色情報を格納することにより、
車線からの逸脱などを検知することもできます。
加えて、周辺の物体の存在確率ではなく、
ロボット自身がそのグリッドに入る確率を、
カルマンフィルタやパーティクルフィルタと同じ
ベイズフィルタの一種である
ヒストグラムフィルタを使って推定することにより、
より高精度でロバスト性の高い自己位置推定を実現することもできます。
(カルマンフィルタやパーティクルフィルタに関しては
下記の記事参考にしてください)
Grid Mapを利用する利点
最後にGrid Mapが自律ロボットに広く使われている理由を説明したいと思います。
1. グリッド探索の計算コストが、グリッドマップのサイズにほどんど関係ない
上記のグリッドの更新方法を見るとわかる通り、
グリッドマップを使用した場合、
地図更新の計算コストはグリッドマップのサイズに
殆ど関係ないことがわかります。
特にEnd Point Updateの場合、
100個のグリッドのグリッドマップでも、
100万個のグリッドのグリッドマップでも、
更新の計算コストは同じです。
(もちろん使用するメモリは大きくなります)
一般的にロボットのソフトウェアにおいては、
メモリよりも計算コストの方が問題になることが多いため、
これは大きな利点になります。
しかし、レイキャスティングの場合は、
各ビンに入るグリッドの数が増えるため、
多少計算コストが上がります。
2. コンピュータに実装しやすい
前述のように、グリッドマップの場合、
最終的なデータは一次元の配列であるため、
非常に簡単にプログラミングできます。
また、グリッドマップのグリッドインデックスの計算も、
上記のように連続値の観測値を線形変換して、
整数型に変換する(整数に丸める)だけで計算できるので、
プログラミング言語で実装しやすいです。
ですので、コンピュータで動くロボットには
実装しやすいとデータ構造・アルゴリズム構造であると言えます。
グリッドマップ以外にも、
ツリー状のデータ構造をした地図表現方法もありますが、
こちらはグリッドマップよりも、
実装が複雑になりがちです。
しかし、3Dのグリッドマップに関しては、
データ量が爆発的に増えてしまうため、
このツリー状のデータを使用した
Octotreeという方法がよく使用されています。
OctoMap - 3D occupancy mapping
3. パスプランニングに利用しやすい
前述の通り、自律移動ロボットにおいて、
作成された地図は主に経路生成に使用されるのですが、
代表的なアルゴリズムであるダイクストラ法やA*は、
このグリッドマップにそのまま応用することができます。
また、前述の通り、ヒストグラムフィルタという
アルゴリズムを使用すると、
ロボットの位置を確率的に推定することができ、
自己位置推定にもグリッドマップを使用することができます。
4. 画像処理の技術を利用できる
グリッドマップは、
見方を変えれば画像と同じデータ構造をしています。
連続値を持つOccupancy Grid Mapは、
データ的にはグレー画像と同じデータ構造をしています。
ですので、これまで画像処理分野で使用されてきた、
計算の高速化の手法や、
特徴点抽出のアルゴリズムなどをそのまま利用することもできます。