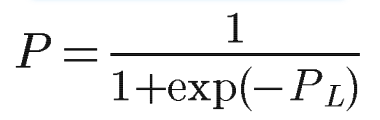はじめに
ロボット工学の論文を読んでいると、
ベイズ理論を使った確率の式が沢山出てきますが、
急に、対数オッズという値が出てくることがあります。
ただでさえも,
よくわからない確率の数式のオンパレードなのにも関わらす、
急に確率の分数のlogが出てくるので、
より一層、論文を読む気がなくなります笑
今回、色々な資料を調べて、
対数オッズを使用する意味や、
その使い方などが、若干わかってきたので
同じ悩みを持っている人向けにメモとして残しておきたいと思います。
対数オッズとは
まず始めに、対数オッズとは、
「確率のオッズの対数をとったもの」
です。
まず初めにオッズとは、
ある確率の表現方法の1つで、
競馬などでもよく使用されています。
オッズ - Wikipedia
ある確率Pがあった時に、
そのオッズは下記の計算式で計算されます。

(このオッズを計算しているので、対数オッズでは分数が出てくるのです。)
このようにオッズは確率1つに対して、1つの値が対応するので、
確率とオッズは同じものの別の表現方法だといえます。
ちなみに、ギャンブルで使用するオッズは
勝率をPとした時の上記の式の値で、
そのギャンブルに勝つと、
元金+元金×1/オッズのお金がもらえることをいいます。
続いて、
このオッズという値の対数をとったものが、
対数オッズです。
この対数オッズと値は、別名ロジットとも呼ばれ、
統計学や確率論でよく使用されています。
以上のように、
対数オッズとは、普通の確率のある一つの表現であり、
複雑な計算の結果として出ているわけではないのです。
ちなみに、対数オッズの値(P_L)を、
通常の確率Pに戻す場合は
下記の式を使って、簡単に復元することができます。
Logit - Wikipedia, the free encyclopedia
対数オッズを使用する意味
続いて、ロボティクスの確率計算の際に、
対数オッズを使用する意味ですが、
大きく分けて2つあります。
一つ目は、
コンピュータを使った時の確率計算の時に生じる
桁落ちの問題を緩和するためです。
まず始めに、確率は一般的に0から1までの範囲を取ります。
続いて、ある確率をオッズで表現することにより、
確率を表すことができる値の範囲が0から∞に広がります。
(上記のオッズの式にPが限りなく1に近い値を代入するとわかるはずです)
続いて、このオッズの値のlogを取ると、
マイナス側にも範囲が広がり -∞から+∞まで範囲が広がります。
(冒頭のグラフはlogのグラフですが、横軸をオッズとして捉えると、
logを取ることにより、縦軸が-∞から+∞の値を取ることがわかると思います)
つまり、ある確率の対数オッズを取る事により、
0-1までの範囲の値を-∞から+∞までに拡張することができるのです。
一般的に、コンピュータで非常に小さい桁数の値を浮動小数点演算すると、
桁数の下の方の値が切り捨てられてしまうことがあります。
特に確率計算の場合は、
0.9999999999のような確率の値を
高速で繰り返し掛け合わせることが多いのですが、
そのような時に、桁落ちが生じて、
確率計算の部分が不安定 (確率の変化が連続的ではなくなる)
になることがあります。
このような通常の確率表現における
0と1付近の計算の不安定性を緩和させるために、
かわりに対数オッズを使用して、
確率の値の範囲を広げているのです。
二つ目の利点は、
確率の更新の計算が掛け算から足し算になるということです。
ロボティクスにおける確率計算では、
ベイズの定理を使用して確率の計算を使用することが多いので、
確率を計算する時には、確率の値を掛け算することが多いです。
(参考:待ち合わせに遅れる彼女、ベイズの定理、そして例題 - MY ENIGMA)
しかし、一般的に掛け算というのは、足し算や引き算と比べて、
計算が遅いことが知られています。
そこで、確率の表現を対数オッズに変えることにより、
学生の時に習った対数の公式を使うことにより、
足し算で確率の更新をすることができます。
確率の計算の回数が少ない場合は、
あまり大きなメリットは得られませんが、
下記のグリッドマップの占有確率などを計算する場合は、
非常に多くの確率を更新しなければならない場合があるため、
結構メリットが大きいようです。
ロボティクスにおける対数オッズの利用例
ロボティクスにおける対数オッズの一番有名な利用例は、
Occupancy Grid Map (OGM)でしょう。
Occupancy grid mapping - Wikipedia, the free encyclopedia
OGMは、
ロボットの周囲をグリッド状に区切り、
それぞれのグリッドの中が占有されているか?
また空いているか?を0-1の確率で表現する方法で、
移動ロボットの分野では、非常に一般的な方法です。
(OGMの詳しい説明は、下記の聖書に詳しく書いてあります。)

確率ロボティクス (Mynavi Advanced Library)
- 作者: Sebastian Thrun,Wolfram Burgard,Dieter Fox
- 出版社/メーカー: マイナビ出版
- 発売日: 2015/04/02
- メディア: Kindle版
- この商品を含むブログを見る

Probabilistic Robotics (INTELLIGENT ROBOTICS AND AUTONOMOUS AGENTS)
- 作者: Sebastian Thrun,Wolfram Burgard,Dieter Fox,Ronald C. Arkin
- 出版社/メーカー: The MIT Press
- 発売日: 2005/08/19
- メディア: ハードカバー
- 購入: 1人 クリック: 6回
- この商品を含むブログを見る
このOGMでは、それぞれのセンサの観測データから
逐次的に大量のグリッドの確率を更新しなければならないのですが、
その確率の計算を、高精度に&効率的に計算するために
対数オッズを使用することが多いようです。
二つ目の利用例はBinary Bayes Filter(BBF)というアルゴリズムです。
BBFはある対象の0-1の状態をベイズフィルタを使って認識するアルゴリズムです。
例えば、あるセンサで観測した物体が、移動物体であるか?
または、その物体がランドマークとして利用できるか?
などを確率的に推定することができます。
(このように考えると、OGMもBBFの一種ですね。)
BBFでも確率の計算を安定に、そして高速に実施するために
対数オッズで確率を計算することが多いようです。
対数オッズを使用したBBFの更新式は
ある時刻tの対数オッズ値をl_tとすると、
となり、足し算で対数オッズを更新することができます。
ちなみに上記の更新式の最後の項は事前確率であり、
BBFでの推定対象が、観測の状態に関係なく、
ある確率になることがわかっている場合の対数オッズになります。
しかし、大抵の場合、推定対象の状態は、観測無しの場合において、
50:50としか言えない場合が多いため、
P(x)=0.5と考えると、最後の項は0になり、無視することができます。
また、対数オッズの最初の初期値は下記の通り、
先ほどの事前確率と同じになります。
以上です。
頭がいい人っているものですね(笑)