目次
はじめに
ロボットの自律移動技術の中で重要な技術の一つに
「経路探索(Path Planning)」がありますが、
今回、その中でも最も基本的な
ダイクストラ法を用いたGrid Map内での
最短経路探索MATLABプログラムを作成したので、
紹介したいと思います。
ダイクストラ法とは?
ダイクストラ法は、
グラフ理論における最短経路探索アルゴリズムの中で
最も古典的な物の一つです。
1959年にエドガーダイクストラによって開発されたものですが、
未だにカーナビの経路探索や、
インターネットのルーティングプログラムに使用されています。
ダイクストラ法の詳細に関しては、
下記のwikiの記事を参照してもらった方が良いと思いますが、
簡単に言うと、
"スタート地点から徐々に探索するノードを拡大させていきながら、
各ノードにおける最小コストを更新していき、
ゴールに着いた時にその最小コストを実現するようなパスを選択する"
アルゴリズムです。
ここにおけるコストは、それぞれの目的によって変わりますが、
例えばある場所までの距離や時間をコストとすることにより、
ダイクストラ法によって、
最も効率的な経路を計算することができるようになります。
ロボットにおける自律移動では、
周辺環境の認識方法として、
周囲の環境を格子状に区切る地図(グリッドマップ)
を使用して、どこが走行可能なのかを判断することが多いです。
なので、この地図を使用して
安全で、効率的な経路を探索することが必要になります。
ダイクストラ法は前述のように、
グラフ理論のアルゴリズムですので、
経路を探索するためには、
経路の候補がグラフ形状で表現されていなければなりません。
グリッドマップでは、
下記の絵のように、あるグリッドに関して
その隣接するグリッド(4 or 8方向)への移動ができるとして、
それらがグラフ状に繋がっていると考える事により、
ダイクストラ法を使用することができます。
ロボットのPath Planningのアルゴリズムとしては、
A*(エースター)というアルゴリズムの方が有名ですが、
A*はこのダイクストラ法を元にしており、
探索するノードの決め方がちょっと違うだけです。
A*に関しては、下記の記事を参照下さい.
ダイクストラ法による経路探索アルゴリズムの流れ
1. ゴールノード(G )とスタートノード(S )を作成する。
また計算中のノードを格納しておくためのリスト(Openリスト)と、
計算済みのノードを格納しておくリスト(Closeリスト)を用意する。
2. スタートノードをOpenリストに追加する、
このときスタートノードの最小コストの推定値
g*(S) = 0 となる。(スター*が付いたものは推定値を表す)
また Closeリストは空にする。
3. Openリストが空なら探索は失敗とする
(スタートからゴールにたどり着くような経路が存在しなかったことになる)。
4. Openリストに格納されているノードn_i を取り出す。
(下記の5-6をすべてのn_iに対して実施する)
5. n_i = G であるなら探索を終了する。それ以外の場合は n_i を Close リストに移す。
6. n_i に隣接している全てのノード(ここでは隣接ノードを m とおく)
に対して以下の操作を行う
6-1. f '(m) = g*(n_i) + COST(n_i,m) を計算する、
ここで, f'(m)はmのコスト値(最小かどうかはまだ不明)
g*(n_i)はノードn_iにおける最小コストの推定値
COST(n_i,m) はノード n_i から m へ移動するときのコストである。
(今回のMALTABプログラムでは方向に関わらず、COST(n_i,m) =1であるとした)
6-2. m の状態に応じて以下の操作を行う
6-2-1. m が Openリストにも Closeリストにも含まれていない場合
f*(m) = f '(m) とし m を Openリストに追加する。
ここで, f*(m)はノードmの最小コスト推定値(更新される可能性あり)
このとき m の親を n として記録する。
6-2-2. m が Openリストにある場合、
f '(m) < f*(m) であるなら f*(m) = f '(m) に置き換える。
(最小コストが更新された)
このとき記録してある m の親を n に置き換える。
6-2-3. m が Closeリストにある場合、
f '(m) < f*(m) であるなら f*(m) = f '(m) として
m を Openリストに移動する。
また記録してある m の親を n に置き換える。
7. 3-6 以降を繰り返す。
8. 探索終了後 G から親を順次たどっていくと S から G までの最短経路が得られる。
運動モデルにおけるコスト設定による複雑な経路探索
非常に単純な自律移動の場合、
ダイクストラ法やA*を使って最短パスを作成し、
それを追従することで自律移動を達成することができます。
しかし、
もう少し高度な自律移動を実現したい時は問題が生じます。
例えば、自動車事故が生じる可能性が最も多いのが
"交差点の右折時"と言われています。
この事実を考慮すると、
自動車の自動走行の場合、
ただ最短経路探索を走るよりも、
"できるだけ右折をしないで、
最短でゴールに向かう経路"を計算したいことがあります。
ダイクストラ法やA*では、
運動モデルにおけるコスト値を調整することで
このような経路を作成することができます。
例えば、今回のMATLABシミュレータの
MotionModel関数の部分で、
X軸(右)方向に向かう運動モデルのコストを非常に大きな値にします。
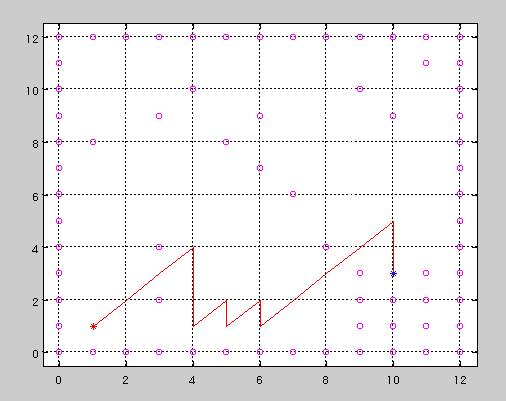
そしてシミュレーションを行った結果が下記です。
この結果を見るとわかる通り、
X軸方向に走行するコストが高いため、
できるだけX軸方向に走らないようにするパスが
選択されていることがわかります。
(東方向に進めないロボットがいるとは思えませんが(笑)...)
このように運動モデルのコスト設定や、
各グリッドのコスト設定を細かく設定することにより、
出来るだけ右折しない経路や、
出来るだけ事故が発生しない場所を走行する経路などを
ダイクストラ法やA*で計算することができるようになります。
ダイクストラ法によるDynamic Programming(動的計画法)
ダイクストラ法やA*を使って、最短経路探索を行う場合、
最初に作成した経路を追従できている時は問題無いのですが、
周辺の状況によって、当初の経路を追従出来ない時があります。
(例えば走ろうとした道が工事中の時など)
そのような時は、ダイクストラ法やA*の場合、
もう一度スタート地点からパスを計算し直す必要がありますが、
スタートとゴールの距離が遠い場合、
非常に計算コストが大きくなってしまいます。
この問題を解決する方法が動的計画法(Dynamic Programming:DP)です。
DPはプログラミングにおける汎用的なアルゴリズムのことですが、
ロボットのPath Planningの分野では、このDPの考え方を使用することにより、
"すべてのノードからゴールまでの最短経路を計算する手法"のことを言います。
今回のMATLABプログラムでは、
ダイクストラ法を用いてDPを実施する関数も実装しました。
下記のプログラムにおいて、
DPWithDijkstraという関数をコメントアウトすると
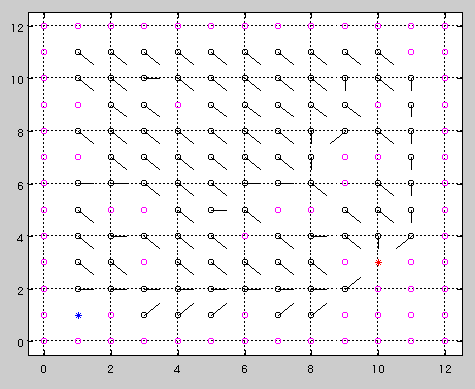
DPを実施し、下記のような結果が得られます。
この結果は、DPにより
すべてのノード(スタート、ゴール、障害物以外)における
ゴールへの最適移動方向を矢印で表しています。
このようにDPによって事前にすべてのノードにおける
最適行動(専門的にはPolicyと言う)を事前に計算しておくことにより、
もし、あるコースが塞がれていて、
当初のコースを追従出来ず、他のノードの位置に行ってしまった時も、
パスの再計算の必要がなく、
そのノードにおける最適行動を実施すれば
ゴールに辿り着くことができるようになります。
MATLABプログラムについて
サンプルプログラムの仕様については、
下記のプログラムを読めばわかると思いますが、
スタートとゴールの位置を指定して、
境界データと障害物データを指定すると、
これらを避けた最短経路を作成してくれます。
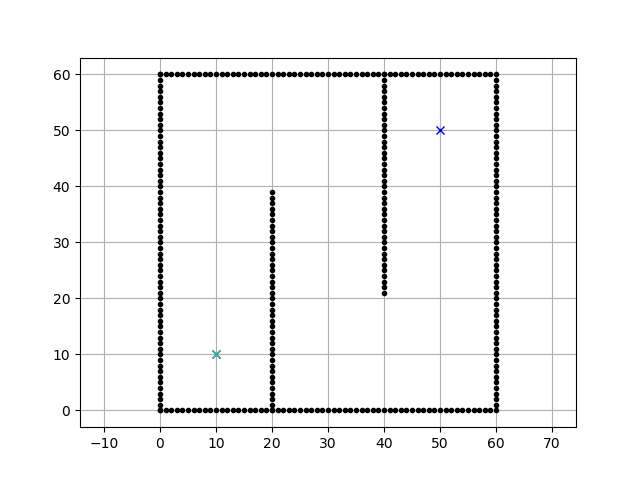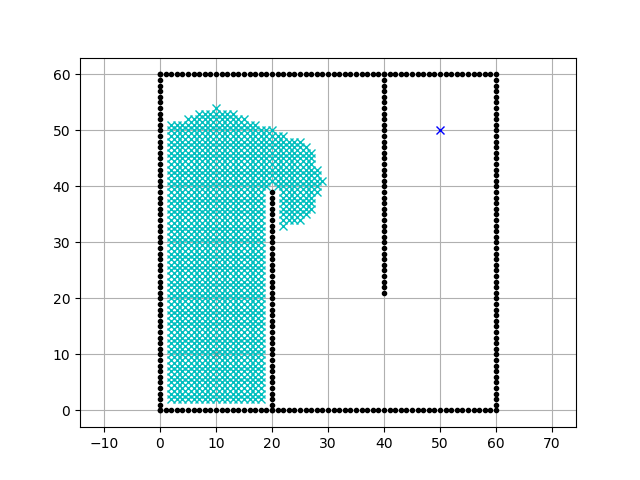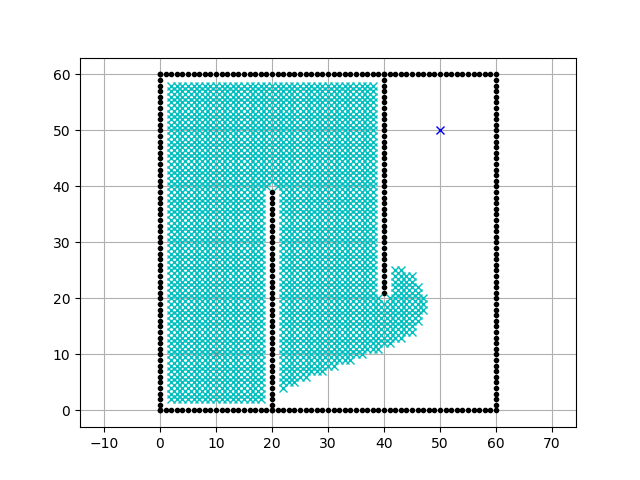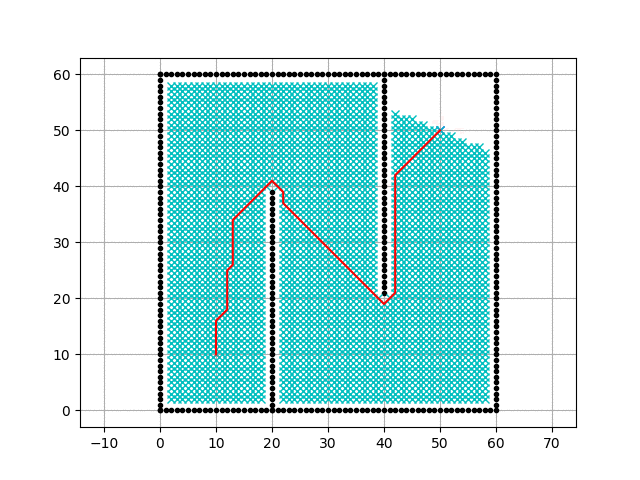
またanimation関数をコメントアウトすることにより、
どのように探索が行われているのかを、
各ステップ毎に確認することができます。
プログラムは下記リンク先のGitHub上にあります。
MATLABRobotics/PathPlanning/Dijkstra/DijkstraSample.m at master · AtsushiSakai/MATLABRobotics