目次
はじめに
以前、自律移動ロボットのPath Planningアルゴリズムとして、
ダイクストラ法や
A*アルゴリズム
を紹介しましたが、これらのアルゴリズムは一般的に、
Global Path Planinngというアルゴリズムに分類されます。
このGlobal Path Planningは、
スタート地点からゴールまでのパスを計算する方法ですが、
いくつか問題点があります。
一つ目は、
ロボットのダイナミクス(運動モデル)を考慮していないということです。
標準的なA*アルゴリズムでは、現在のロボットの速度や運動モデルは考慮せず、
単純に隣接グリッド間の移動が最小になるようなパスを計算します。
しかし実際には、ステアリング型のロボットなど、
横方法に簡単に旋回できないロボットの場合、
安全が担保されたパスを生成したにも関わらず、
そのパスに追従できずに、障害物に衝突してしまうということが発生します。
二つ目は、計算コストが大きいということです。
パスを引くスタート地点とゴール地点が遠い場合、
グリッドの解像度にもよりますが、計算コストは莫大になります。
従って、毎回の制御ループ時に
パスを再計算(Replanning)をすることが難しいという問題があります。
これは移動物体などが存在する動的環境での自律移動の際に、
非常に大きな問題になります。
Replanningが間に合わないままのパスで走行すると、
動的物体を考慮しないまま走行してしまうので、
最悪の場合、動的物体に衝突してしまうのです。
以上のようなGlobal Path Planningの問題を解決する方法が
Local Path Planningと呼ばれるアルゴリズムです。
Local Path Planningは、ロボットのダイナミクスを考慮した上で、
比較的近い距離までのパスプランニングを高速に実施するための
アルゴリズムです。
Global Path Planningでは、計算結果としてパス(x-yの位置情報)が
出力されますが、
Local Path Planningでは、車体のダイナミクスを考慮しているため、
最終的な制御入力(前進速度やステアリング角度)まで計算します。
しかし、Local Path Planningは計算コストの問題で、
非常に近い距離までしかパスを引くことができないので、
局所解(行き止まりなど)でパスが引けなくなるという問題があります。
したがって、一般的にはGlobal Path Planningと
Local Path Planningを組み合わせてシステムを構築します。
(A*で引いたパスを追従するようにLocal Path Planningで制御入力を計算するなど)
今回はLocal Path Planningの代表的なアルゴリズムである
Dynamic Window Approachの簡単な説明と、
MALTAB, Python サンプルプログラムを紹介したいと思います。
Dynamic Window Approachとは、
Dynamic Window Approach:DWAは1997年に有名なロボティクスの教科書である
『確率ロボティクス』の著者の人達が提案した
Local Path Planningアルゴリズムです。
論文リンク:Dynamic Window Approach to Collision Avoidance
非常に単純なアルゴリズムでありながらも、
ロボットの運動モデルを考慮したパスを
高速に生成し、最終的なな制御入力まで計算できることから、
多くのロボットで使用されています。
特に、動的環境を走行する屋内ロボットにおいては、
広く利用されており、ROSのデフォルトパッケージである、
Navigationのbase_local_plannerも
DWAを元にしたソフトになっています。
DWAの詳しいアルゴリズムは、
上記の論文とMATLABサンプルプログラムを参照して頂きたいのですが、
簡単にDWAのアルゴリズムの流れを説明したいと思います。
DWAは、現在の位置情報と速度情報、障害物情報、
そしてゴールの位置情報から、
ロボットの運動モデルに則した制御入力を計算してくれます。
今回のサンプルプログラムでは、
一般的な差動二輪運動モデルを元に、
制御入力を前進速度v、回頭速度ωの2つとして
次の時刻に入力すべき最適な制御入力を計算します。
一言でDWAのアルゴリズムを説明すると、
“現在のロボットの速度とロボットの運動モデルから
次の時刻までに取りうるロボットの制御入力の範囲
(Dynamic Window)を計算し、
その範囲内の制御入力をサンプリングして、
事前に決めた評価関数が最大になる制御入力を計算する”
アルゴリズムだと言えます。
もう少し詳細を説明しましょう。
DWAは大きくわけて下記の2つのプロセスから、
安全で最適な制御入力を計算します。
1.Dynamic Windowの計算
2.評価関数の最適化
1. Dynamic WIndowの計算
前述のように、Dynamic Windowとは、
次の時刻にロボットが実施できる
制御入力の範囲のことを言います。
Dynamic Windowは
下記の3種類のWindowのANDを取ったものになります。
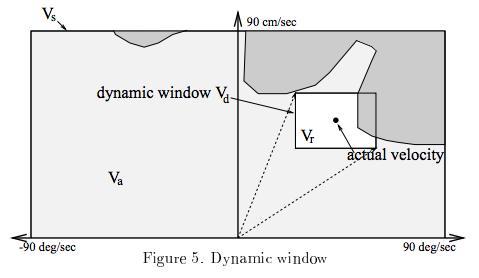
下記の論文の図を元に説明したいと思います。
・Window 1: 制御可能範囲
これは、上図でいう所のVsに対応し、
ロボットが取りうる制御入力の最大値と最小値
の範囲を意味します。
そもそもロボットにおいては、モータのスペックなどで
最高速や最高回頭速度が決っているので、
この値を使用することになります。
・Window 2: 動的制御可能範囲
これは上図で言う所のVrに対応し、
現在の速度と、スペック上での最大加減速度を元に計算された
次の時刻までに取りうる最大最小の制御入力のことです。
このように最大加減速を考慮することで、
ロボットのスペックに応じた制御入力を探索することができます。
・Window 3: 障害物による許容制御入力
これは上図で言う所のVaに対応し、
障害物センサによる観測結果と、
ロボットの最大減速度の値から計算される、
安全に走行できる制御入力の範囲になります。
このようなWindowを設定することで、
モデルが正確であれば、障害物にはぶつからない
制御入力のみを探索することができます。
以上の3つの制御入力の範囲(Window)の
重なる部分の制御入力の範囲のみ
を考えることにより、
安全で、かつ、ロボットの運動モデルを考慮した
制御入力のみを利用することができるのです。
2. 評価関数の最適化
続いて、先ほどのDynamic Windowの制御範囲を
ある一定値毎にサンプリングします。
このサンプリング値は、ロボットが制御可能な制御解像度を与えます。
しかし、この解像度を小さくし過ぎると、
計算コストが増大するので注意が必要です。
続いて、それぞれのサンプリング制御値に関して
下記の評価関数を計算します。

まず一つ目の項、heading(v,ω)は、
その制御入力の時のロボットの方位とゴール方向の差の角度を180度から引いた値です。
ゴールに真っ直ぐ向かっている場合は、評価値が大きくなります。
二つ目の項dist(v,ω)は、
その制御入力の時の、最近傍の障害物までの距離を表します。
障害物から遠い制御入力の評価値が大きくなります。
三つ目の項velocity(v,ω)は、
単純に制御入力のvの値を使用します。
速度が早い制御入力の評価値が大きくなります。
α、β、γはそれぞれの項の線形足しあわせの重みパラメータです。
これらのパラメータを調整することにより、
ゴールに向かいつつ、障害物を避けながら、高速に走ることができる
制御入力が逐次的に計算されるようになるのです。
また最後のσはスムージング関数です。
制御入力が近いサンプリング値の評価値の平均などをとって、
滑らかにさせるための関数です。
今回のサンプルコードでは、このスムージングは実施していません。
最後にそれぞれの制御サンプリング値において
この評価値を計算し、その中で一番評価値が大きい制御入力を
最適値として採用します。
以上のような方法でDWAでは、
高速に最適な制御入力を計算するのです。
DWAの利点と欠点
DWAには
下記のような利点と欠点があります。
利点
- 高速な計算が可能 (10ms以下)
- 車両モデルを取り入れることができる
- パラメータをチューニングしやすい
- Global Dynamic Window approachを使えば、局所コースに陥らずにすむ
欠点
- 通常のDWAのアルゴリズムでは、局所コースに陥ってしまう。
- 一定制御入力という仮定があるため、複雑な走行ができない
DWAのMATLABサンプルプログラム
下記がMATLABサンプルプログラムです。
% ------------------------------------------------------------------------- % % File : DynamicWindowApproachSample.m % % Discription : Mobile Robot Motion Planning with Dynamic Window Approach % % Environment : Matlab % % Author : Atsushi Sakai % % Copyright (c): 2014 Atsushi Sakai % % ------------------------------------------------------------------------- function [] = DynamicWindowApproachSample() close all; clear all; disp('Dynamic Window Approach sample program start!!') x=[0 0 pi/2 0 0]';%ロボットの初期状態[x(m),y(m),yaw(Rad),v(m/s),ω(rad/s)] goal=[10,10];%ゴールの位置 [x(m),y(m)] %障害物リスト [x(m) y(m)] obstacle=[0 2; 4 2; 4 4; 5 4; 5 5; 5 6; 5 9 8 8 8 9 7 9]; obstacleR=0.5;%衝突判定用の障害物の半径 global dt; dt=0.1;%刻み時間[s] %ロボットの力学モデル %[最高速度[m/s],最高回頭速度[rad/s],最高加減速度[m/ss],最高加減回頭速度[rad/ss], % 速度解像度[m/s],回頭速度解像度[rad/s]] Kinematic=[1.0,toRadian(20.0),0.2,toRadian(50.0),0.01,toRadian(1)]; %評価関数のパラメータ [heading,dist,velocity,predictDT] evalParam=[0.1,0.2,0.1,3.0]; area=[-1 11 -1 11];%シミュレーションエリアの広さ [xmin xmax ymin ymax] %シミュレーション結果 result.x=[]; tic; %movcount=0; % Main loop for i=1:5000 %DWAによる入力値の計算 [u,traj]=DynamicWindowApproach(x,Kinematic,goal,evalParam,obstacle,obstacleR); x=f(x,u);%運動モデルによる移動 %シミュレーション結果の保存 result.x=[result.x; x']; %ゴール判定 if norm(x(1:2)-goal')<0.5 disp('Arrive Goal!!');break; end %====Animation==== hold off; ArrowLength=0.5;%矢印の長さ %ロボット quiver(x(1),x(2),ArrowLength*cos(x(3)),ArrowLength*sin(x(3)),'ok');hold on; plot(result.x(:,1),result.x(:,2),'-b');hold on; plot(goal(1),goal(2),'*r');hold on; plot(obstacle(:,1),obstacle(:,2),'*k');hold on; %探索軌跡表示 if ~isempty(traj) for it=1:length(traj(:,1))/5 ind=1+(it-1)*5; plot(traj(ind,:),traj(ind+1,:),'-g');hold on; end end axis(area); grid on; drawnow; %movcount=movcount+1; %mov(movcount) = getframe(gcf);% アニメーションのフレームをゲットする end figure(2) plot(result.x(:,4)); toc %movie2avi(mov,'movie.avi'); function [u,trajDB]=DynamicWindowApproach(x,model,goal,evalParam,ob,R) %DWAによる入力値の計算をする関数 %Dynamic Window[vmin,vmax,ωmin,ωmax]の作成 Vr=CalcDynamicWindow(x,model); %評価関数の計算 [evalDB,trajDB]=Evaluation(x,Vr,goal,ob,R,model,evalParam); if isempty(evalDB) disp('no path to goal!!'); u=[0;0];return; end %各評価関数の正規化 evalDB=NormalizeEval(evalDB); %最終評価値の計算 feval=[]; for id=1:length(evalDB(:,1)) feval=[feval;evalParam(1:3)*evalDB(id,3:5)']; end evalDB=[evalDB feval]; [maxv,ind]=max(feval);%最も評価値が大きい入力値のインデックスを計算 u=evalDB(ind,1:2)';%評価値が高い入力値を返す function [evalDB,trajDB]=Evaluation(x,Vr,goal,ob,R,model,evalParam) %各パスに対して評価値を計算する関数 evalDB=[]; trajDB=[]; for vt=Vr(1):model(5):Vr(2) for ot=Vr(3):model(6):Vr(4) %軌跡の推定 [xt,traj]=GenerateTrajectory(x,vt,ot,evalParam(4),model); %各評価関数の計算 heading=CalcHeadingEval(xt,goal); dist=CalcDistEval(xt,ob,R); vel=abs(vt); evalDB=[evalDB;[vt ot heading dist vel]]; trajDB=[trajDB;traj]; end end function EvalDB=NormalizeEval(EvalDB) %評価値を正規化する関数 if sum(EvalDB(:,3))~=0 EvalDB(:,3)=EvalDB(:,3)/sum(EvalDB(:,3)); end if sum(EvalDB(:,4))~=0 EvalDB(:,4)=EvalDB(:,4)/sum(EvalDB(:,4)); end if sum(EvalDB(:,5))~=0 EvalDB(:,5)=EvalDB(:,5)/sum(EvalDB(:,5)); end function [x,traj]=GenerateTrajectory(x,vt,ot,evaldt,model) %軌跡データを作成する関数 global dt; time=0; u=[vt;ot];%入力値 traj=x;%軌跡データ while time<=evaldt time=time+dt;%シミュレーション時間の更新 x=f(x,u);%運動モデルによる推移 traj=[traj x]; end function stopDist=CalcBreakingDist(vel,model) %現在の速度から力学モデルに従って制動距離を計算する関数 global dt; stopDist=0; while vel>0 stopDist=stopDist+vel*dt;%制動距離の計算 vel=vel-model(3)*dt;%最高原則 end function dist=CalcDistEval(x,ob,R) %障害物との距離評価値を計算する関数 dist=2; for io=1:length(ob(:,1)) disttmp=norm(ob(io,:)-x(1:2)')-R;%パスの位置と障害物とのノルム誤差を計算 if dist>disttmp%最小値を見つける dist=disttmp; end end function heading=CalcHeadingEval(x,goal) %headingの評価関数を計算する関数 theta=toDegree(x(3));%ロボットの方位 goalTheta=toDegree(atan2(goal(2)-x(2),goal(1)-x(1)));%ゴールの方位 if goalTheta>theta targetTheta=goalTheta-theta;%ゴールまでの方位差分[deg] else targetTheta=theta-goalTheta;%ゴールまでの方位差分[deg] end heading=180-targetTheta; function Vr=CalcDynamicWindow(x,model) %モデルと現在の状態からDyamicWindowを計算 global dt; %車両モデルによるWindow Vs=[0 model(1) -model(2) model(2)]; %運動モデルによるWindow Vd=[x(4)-model(3)*dt x(4)+model(3)*dt x(5)-model(4)*dt x(5)+model(4)*dt]; %最終的なDynamic Windowの計算 Vtmp=[Vs;Vd]; Vr=[max(Vtmp(:,1)) min(Vtmp(:,2)) max(Vtmp(:,3)) min(Vtmp(:,4))]; %[vmin,vmax,ωmin,ωmax] function x = f(x, u) % Motion Model global dt; F = [1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0]; B = [dt*cos(x(3)) 0 dt*sin(x(3)) 0 0 dt 1 0 0 1]; x= F*x+B*u; function radian = toRadian(degree) % degree to radian radian = degree/180*pi; function degree = toDegree(radian) % radian to degree degree = radian/pi*180;
下記のGitHubリポジトリにて公開しています。
使い方はコードをちょっと見てもらえればわかると思いますが、
プログラムの冒頭のパラメータを設定すれば、
障害物を避けるようにDWAで走行するはずです。
ただ、あまりにも障害物を置き過ぎると
すぐに局所解に陥ってしまうので注意しましょう。
Pythonサンプルプログラム
下記はDWAのPythonサンプルプログラムです。
""" Mobile robot motion planning sample with Dynamic Window Approach author: Atsushi Sakai (@Atsushi_twi) """ import math import numpy as np import matplotlib.pyplot as plt show_animation = True class Config(): # simulation parameters def __init__(self): # robot parameter self.max_speed = 1.0 # [m/s] self.min_speed = -0.5 # [m/s] self.max_yawrate = 40.0 * math.pi / 180.0 # [rad/s] self.max_accel = 0.2 # [m/ss] self.max_dyawrate = 40.0 * math.pi / 180.0 # [rad/ss] self.v_reso = 0.01 # [m/s] self.yawrate_reso = 0.1 * math.pi / 180.0 # [rad/s] self.dt = 0.1 # [s] self.predict_time = 3.0 # [s] self.to_goal_cost_gain = 1.0 self.speed_cost_gain = 1.0 self.robot_radius = 1.0 # [m] def motion(x, u, dt): # motion model x[2] += u[1] * dt x[0] += u[0] * math.cos(x[2]) * dt x[1] += u[0] * math.sin(x[2]) * dt x[3] = u[0] x[4] = u[1] return x def calc_dynamic_window(x, config): # Dynamic window from robot specification Vs = [config.min_speed, config.max_speed, -config.max_yawrate, config.max_yawrate] # Dynamic window from motion model Vd = [x[3] - config.max_accel * config.dt, x[3] + config.max_accel * config.dt, x[4] - config.max_dyawrate * config.dt, x[4] + config.max_dyawrate * config.dt] # print(Vs, Vd) # [vmin,vmax, yawrate min, yawrate max] dw = [max(Vs[0], Vd[0]), min(Vs[1], Vd[1]), max(Vs[2], Vd[2]), min(Vs[3], Vd[3])] return dw def calc_trajectory(xinit, v, y, config): x = np.array(xinit) traj = np.array(x) time = 0 while time <= config.predict_time: x = motion(x, [v, y], config.dt) traj = np.vstack((traj, x)) time += config.dt return traj def calc_final_input(x, u, dw, config, goal, ob): xinit = x[:] min_cost = 10000.0 min_u = u min_u[0] = 0.0 best_traj = np.array([x]) # evalucate all trajectory with sampled input in dynamic window for v in np.arange(dw[0], dw[1], config.v_reso): for y in np.arange(dw[2], dw[3], config.yawrate_reso): traj = calc_trajectory(xinit, v, y, config) # calc cost to_goal_cost = calc_to_goal_cost(traj, goal, config) speed_cost = config.speed_cost_gain * \ (config.max_speed - traj[-1, 3]) ob_cost = calc_obstacle_cost(traj, ob, config) #print(ob_cost) final_cost = to_goal_cost + speed_cost + ob_cost # search minimum trajectory if min_cost >= final_cost: min_cost = final_cost min_u = [v, y] best_traj = traj return min_u, best_traj def calc_obstacle_cost(traj, ob, config): # calc obstacle cost inf: collistion, 0:free skip_n = 2 minr = float("inf") for ii in range(0, len(traj[:, 1]), skip_n): for i in range(len(ob[:, 0])): ox = ob[i, 0] oy = ob[i, 1] dx = traj[ii, 0] - ox dy = traj[ii, 1] - oy r = math.sqrt(dx**2 + dy**2) if r <= config.robot_radius: return float("Inf") # collision if minr >= r: minr = r return 1.0 / minr # OK def calc_to_goal_cost(traj, goal, config): # calc to goal cost. It is 2D norm. goal_magnitude = math.sqrt(goal[0]**2 + goal[1]**2) traj_magnitude = math.sqrt(traj[-1, 0]**2 + traj[-1, 1]**2) dot_product = (goal[0]*traj[-1, 0]) + (goal[1]*traj[-1, 1]) error = dot_product / (goal_magnitude*traj_magnitude) error_angle = math.acos(error) cost = config.to_goal_cost_gain * error_angle return cost def dwa_control(x, u, config, goal, ob): # Dynamic Window control dw = calc_dynamic_window(x, config) u, traj = calc_final_input(x, u, dw, config, goal, ob) return u, traj def plot_arrow(x, y, yaw, length=0.5, width=0.1): plt.arrow(x, y, length * math.cos(yaw), length * math.sin(yaw), head_length=width, head_width=width) plt.plot(x, y) def main(): print(__file__ + " start!!") # initial state [x(m), y(m), yaw(rad), v(m/s), omega(rad/s)] x = np.array([0.0, 0.0, math.pi / 8.0, 0.0, 0.0]) # goal position [x(m), y(m)] goal = np.array([10, 10]) # obstacles [x(m) y(m), ....] ob = np.matrix([[-1, -1], [0, 2], [4.0, 2.0], [5.0, 4.0], [5.0, 5.0], [5.0, 6.0], [5.0, 9.0], [8.0, 9.0], [7.0, 9.0], [12.0, 12.0] ]) u = np.array([0.0, 0.0]) config = Config() traj = np.array(x) for i in range(1000): u, ltraj = dwa_control(x, u, config, goal, ob) x = motion(x, u, config.dt) traj = np.vstack((traj, x)) # store state history if show_animation: plt.cla() plt.plot(ltraj[:, 0], ltraj[:, 1], "-g") plt.plot(x[0], x[1], "xr") plt.plot(goal[0], goal[1], "xb") plt.plot(ob[:, 0], ob[:, 1], "ok") plot_arrow(x[0], x[1], x[2]) plt.axis("equal") plt.grid(True) plt.pause(0.0001) # check goal if math.sqrt((x[0] - goal[0])**2 + (x[1] - goal[1])**2) <= config.robot_radius: print("Goal!!") break print("Done") if show_animation: plt.plot(traj[:, 0], traj[:, 1], "-r") plt.show() if __name__ == '__main__': main()
下記のGitHubリポジトリでも公開しています。
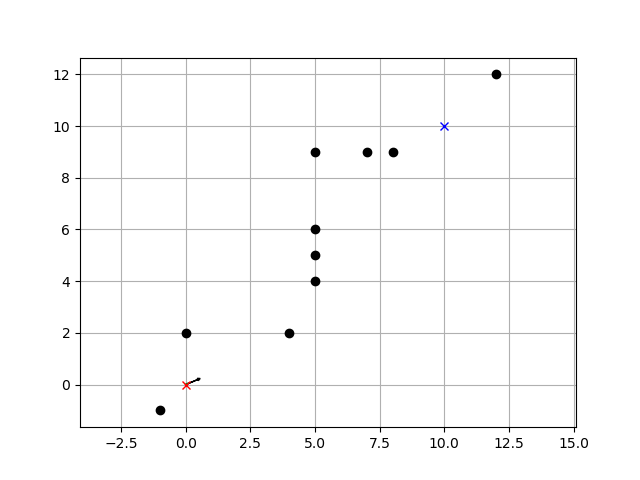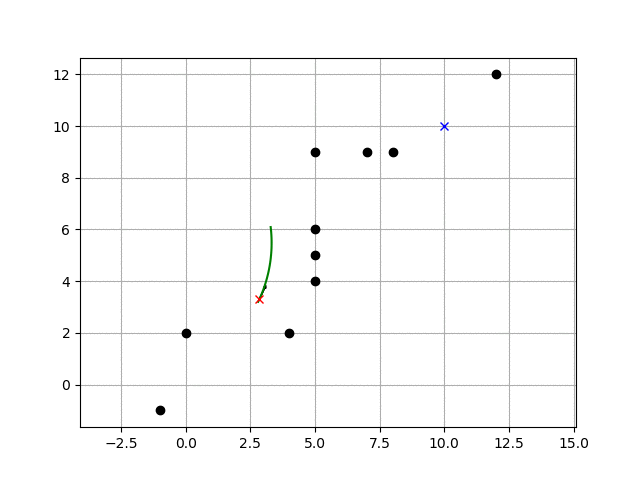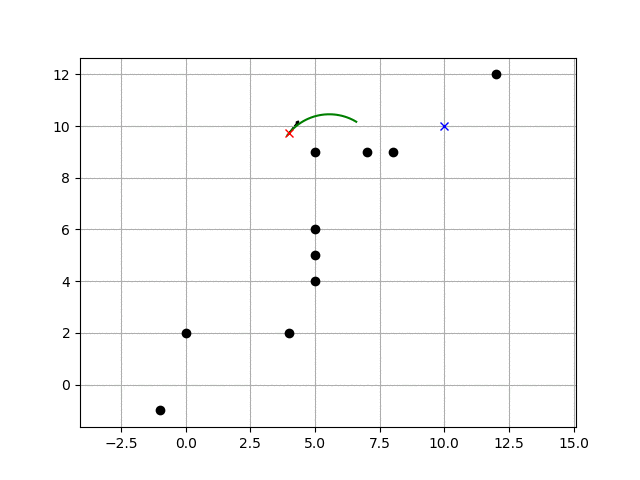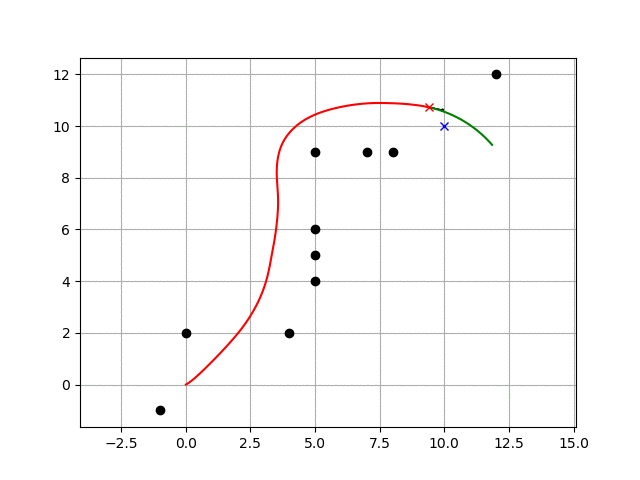
上記コードを実行すると、
冒頭の動画ようなシミュレーションが実行されます。