はじめに

これまで

様々な最適化の手法や、

myenigma.hatenablog.com

それを利用した制御手法である

モデル予測制御の概要を説明してきましたが、

myenigma.hatenablog.com

今回は、下記の論文を元にして、

MIXED INTEGER PROGRAMMING FOR MULTI-VEHICLE PATH PLANNING

Mixed Integer Programming(整数計画法)によるモデル予測制御技術の概要の説明と、

Juliaによるシンプルなシミュレーションを紹介したいと思います。

混合整数計画法に関しては、下記を参照ください。

speakerdeck.com

Mixed Integer Programming(整数計画法)によるモデル予測制御技術

今回は、下記の論文を元にして、

MIXED INTEGER PROGRAMMING FOR MULTI-VEHICLE PATH PLANNING

四角で表された障害物を回避しながら、

ゴール地点に向かう

モデル予測制御アルゴリズムを実装したいと思います。

この論文では、

スラック変数を使って、

線形運動モデルのロボットを、

下記のように線形計画問題として定式化し、

f:id:meison_amsl:20171028125551p:plain

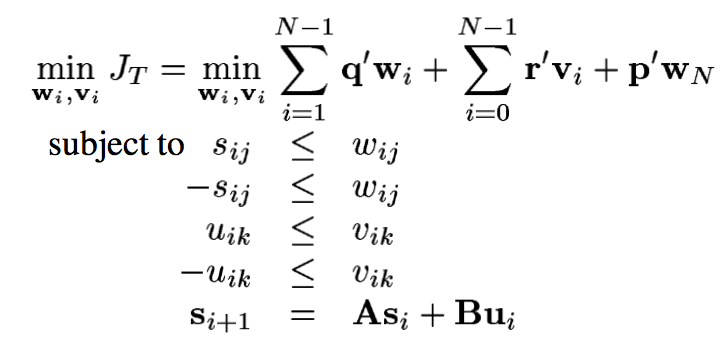
障害物回避は下記のように、

Mixed Integer Programming(整数計画法)として

定式化しています。

f:id:meison_amsl:20171028125603p:plain

上記の式を組み合わせることで、

障害物を回避しながら、

できるだけゴールに近づき、

かつ入力を減らすように走行できます。

上記の最適化計算を、

あるホライズン数分だけ実施し、

最適化計算の結果の入力プロファイルの

初めの入力値を実際に利用する

Receding Horizon 制御を実施します。

詳細は前述の論文を参照ください。

Juliaによるシンプルなサンプルプログラム

今回、JuliaとJulia製の最適化ライブラリJuMPを使って、

前述のモデル予測制御のシミュレーションをしてみました。

myenigma.hatenablog.com

下記がシミュレーションコードです。

今回運動モデルとしては、単純なDouble Integratorを使用し、

x,yの入力に制約条件をいれています。

#
# A path planning code based on mix integer optimization
#
# author: Atsushi Sakai(@Atsushi_twi)
#

using PyCall
using JuMP
using CPLEX

@pyimport matplotlib.pyplot as plt

solver = CplexSolver(CPX_PARAM_SCRIND=0)

const A = [1.0 0.0;
        0.0 1.0]
const B = [1.0 1.0;
        0.0 1.0]
const q = [1.0; 1.0]
const r = [1.0; 1.0]

const u_max = 0.1
const T = 50
const M = 10000.0

function control(is, gs, ob)

    nob = length(ob[:,1])

    model = Model(solver=solver)
    @variable(model, w[1:2,t=1:T])
    @variable(model, v[1:2,t=1:T])
    @variable(model, s[1:2,t=1:T])
    @variable(model, -u_max <= u[1:2,t=1:T] <= u_max)
    @variable(model, o[1:4*nob,t=1:T], Bin)

    @constraint(model, s[:,1] .== is)

    obj = []
    for i in 1:T
        @constraint(model, s[:,i] - gs .<= w[:,i])
        @constraint(model, -s[:,i] + gs .<= w[:,i])
        @constraint(model, u[:,i] .<= v[:,i])
        @constraint(model, -u[:,i] .<= v[:,i])
        push!(obj, q'*w[1:end,i]+r'*v[1:2,i])


        # obstable avoidanse
        for io in 1:nob
            start_ind = 1+(io-1)*4
            @constraint(model, sum(o[start_ind:start_ind+3, i]) <= 3)
            @constraint(model, s[1,i] <= ob[io, 1] + M * o[start_ind, i])
            @constraint(model, -s[1,i] <= -ob[io, 2] + M * o[start_ind+1, i])
            @constraint(model, s[2,i] <= ob[io, 3] + M * o[start_ind+2, i])
            @constraint(model, -s[2,i] <= -ob[io, 4] + M * o[start_ind+3, i])
        end
    end

    for i in 1:T-1
        @constraint(model, s[:,i+1] .== A*s[:,i]+B*u[:,i])
    end

    @objective(model, Min, sum(obj))

    status = solve(model)

    u_vec = getvalue(u)
    s_vec = getvalue(s)

    return s_vec, u_vec
end

function plot_obstacle(ob)
    for i in 1:length(ob[:,1])
        x = [ob[i,1],ob[i,2],ob[i,2],ob[i,1],ob[i,1]]
        y = [ob[i,3],ob[i,3],ob[i,4],ob[i,4],ob[i,3]]
        plt.plot(x,y,"-g")
    end
end

function main()
    println(PROGRAM_FILE," start!!")

    s = [10.0, 5.0] # init state
    gs = [5.0, 7.0] # goal state

    ob = [7.0 8.0 3.0 8.0;
         5.5 6.0 6.0 10.0;] # [xmin xmax ymin ymax]

    h_sx = []
    h_sy = []

    for i=1:10000
        s_p, u_p = control(s, gs, ob)

        if sqrt((gs[1]-s[1])^2+(gs[2]-s[2])^2) <= 0.1
            println("Goal!!!")
            break
        end

        s = A*s+B*u_p[:,1] # simulation

        push!(h_sx, s[1])
        push!(h_sy, s[2])

        plt.cla()
        plt.plot(gs[1],gs[2],"*r")
        plt.plot(s_p[1,:],s_p[2,:],"xb")
        plot_obstacle(ob)
        plt.plot(s_p[1,:],s_p[2,:],"xb")
        plt.plot(h_sx,h_sy,"-b")
        plt.plot(s[1],s[2],"or")
        plt.axis("equal")
        plt.grid(true)
        plt.pause(0.0001)

    end

    plt.cla()
    plot_obstacle(ob)
    plt.plot(gs[1],gs[2],"*r")
    plt.plot(h_sx,h_sy,"-b")
    plt.axis("equal")
    plt.grid(true)
    plt.show()

    println(PROGRAM_FILE," Done!!")
end


if contains(@__FILE__, PROGRAM_FILE)
    @time main()
end