はじめに

最近、ロボットの制御や経路生成の勉強をしているのですが、

しばしば出てくる技術として、

線形二次レギュレータ(Linear-Quadratic Regulator:LQR)があります。

今回はこのLQRの概要とLQRによる

簡単なPython制御シミュレーションコードを紹介したいと思います。

LQRの概要

LQRは最適制御と呼ばれれる制御手法の一つです。

Linear–quadratic regulator - Wikipedia

下記のような線形システムに対して、

f:id:meison_amsl:20161105031626p:plain

下記のようなコスト関数を最小するための最適入力u*を計算することができます。

f:id:meison_amsl:20161105031924p:plain

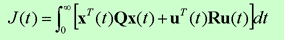
最適入力u*は状態ベクトルxに対するゲインKを使って、

下記の式で計算できます。

f:id:meison_amsl:20161105032041p:plain

このゲインKは下記の式で計算できます

まず初めにリッカチ方程式を解きます。

リッカチの微分方程式 - Wikipedia

上記のコスト関数におけるリッカチの微分方程式の解き方としては、

Xの初期値をQとして、

下記の式でXを複数回更新し、

Xが変化しなくなるまで計算した値を利用します。

$X = A^T X A - A^T X B(R + B^TXB)^{-1}B^T X A + Q$

解のXの値から、下記の式でゲインを計算できます。

f:id:meison_amsl:20161105032948p:plain

つまり、自分の解きたい問題に対して、

上手く上記の式にモデルを設定することで、

解析的に最適入力を計算することができるのです。

一つ重要な点として、

線形方程式のA,B,Cの要素やコスト行列が変化しない場合、

LQRのゲインは変わりません。

従って、下記のシミュレーションでも実施している通り、

リッカチの方程式を解いてゲインを計算するのは、

モデルが変わらない場合、初めの一回だけでOKです。

Kと現在の状態x_tを掛け合わせるだけで、

その時々の最適入力を計算することができます。

PythonによるLQRの制御シミュレーション

下記が簡単なLQRのPython制御シミュレーションのコードです。

""" 
Linear-Quadratic Regulator sample code
author Atsushi Sakai
"""

import matplotlib.pyplot as plt
import numpy as np
import scipy.linalg as la

simTime = 3.0
dt = 0.1

# x[k+1] = Ax[k] + Bu[k]
# y[k] = Cx[k]
A = np.matrix([[1.1, 2.0], [0, 0.95]])
B = np.matrix([0.0, 0.0787]).T
C = np.matrix([-2, 1])
Kopt = None


def observation(x):
    y = C * x
    ry = float(y[0])
    return (ry)


def process(x, u):
    x = A * x + B * u
    return (x)


def solve_DARE(A, B, Q, R):
    """
    solve a discrete time_Algebraic Riccati equation (DARE)
    """
    X = Q
    maxiter = 150
    eps = 0.01

    for i in range(maxiter):
        Xn = A.T * X * A - A.T * X * B * la.inv(R + B.T * X * B) * B.T * X * A + Q
        if (abs(Xn - X)).max() < eps:
            X = Xn
            break
        X = Xn

    return Xn


def dlqr(A, B, Q, R):
    """Solve the discrete time lqr controller.
    x[k+1] = A x[k] + B u[k]
    cost = sum x[k].T*Q*x[k] + u[k].T*R*u[k]
    # ref Bertsekas, p.151
    """

    # first, try to solve the ricatti equation
    X = solve_DARE(A, B, Q, R)

    # compute the LQR gain
    K = np.matrix(la.inv(B.T * X * B + R) * (B.T * X * A))

    eigVals, eigVecs = la.eig(A - B * K)

    return K, X, eigVals


def lqr_control(x):
    global Kopt
    if Kopt is None:
        Kopt, X, ev = dlqr(A, B, C.T * np.eye(1) * C, np.eye(1))

    u = -Kopt * x
    return u


def main():
    time = 0.0
    u_history = []
    y_history = []
    time_history = []

    x = np.matrix([3, 1]).T
    u = np.matrix([0, 0, 0])

    while time <= simTime:
        u = lqr_control(x)
        u0 = float(u[0, 0])
        x = process(x, u0)
        y = observation(x)

        u_history.append(u0)
        y_history.append(y)
        time_history.append(time)
        time += dt

    plt.plot(time_history, u_history, "-r", label="input")
    plt.plot(time_history, y_history, "-b", label="output")
    plt.grid(True)
    plt.xlim([0, simTime])
    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()