目次
はじめに
最新のロボット技術の重要な技術として、
確率・統計の技術も重要ですが、
もう一つよく利用されるのが最適化技術です。
特に、パスプランニングや制御などでよく利用されます。
近年は様々なプラットフォームで利用可能な、
最適化ツール(ソルバー)が気軽に利用できるので、
ソルバーにデータを入れれば
求めている答えを得ることができることも多いです。
しかし、やはりそのようなツールを使うとしても、
背景にある技術を知ることも重要だと思うので、
自分で少し勉強した内容をまとめておきたいと思います。
下記で述べる内容は基本的に下記の資料を参考にまとめました。
いずれも素晴らしい資料ですので、
より詳しく学びたい方は下記の資料を参考にしてもらえると良いと思います。

- 作者:Boyd, Stephen,Vandenberghe, Lieven
- 発売日: 2004/03/08
- メディア: ハードカバー

- 作者:健一, 金谷
- 発売日: 2005/09/01
- メディア: 単行本
最適化とは?
最適化は、ある入力に対して、
その入力を元に計算される評価関数を最小化(最大化)する
入力を計算することです。
この最適化を実現するには、様々な定式化の方法が考えられますが、
一般的に下記の定式を利用することが多いようです。

それぞれの記号の意味は下記の通りです。

xはベクトルで複数の入力値を表しています。
foは評価関数(コスト関数)で、
foを最小化するxを求めるのが最適化の目的になります。
fiは制約条件(constraints)です。
最適化問題によっては、
この制約条件が無い場合もありますが、
一般的には、入力のxはある範囲の条件を持ったり、
入力同士である条件を満たす必要があったりします。
つまり、fiの制約条件を満たした状態で、
foを最小化するxを求めるのが、最適化だということです。
上記の問題を解くために様々な技術が研究、開発されています。
最適化の応用例
この最適化技術は様々な用途で利用されています。
ポートフォリオ最適化
ポートフォリオ最適化は、経済学でしばしば利用される技術で、
様々な投資資産の量を入力とし、
リスクとリターンのバランスを最適化するのに利用されています。
制約条件としては、投資予算や、
各投資資産の最大最小値などが設定されるようです。
電子回路における部品サイズの最適化
電子回路を設計する上で、
様々な部品のサイズを入力にし、
消費電力を最小化するような最適化をすることで、
電子回路の設計をする場合も多いようです。
制約条件としては、部品のサイズの最大最小値などが利用されます。
データフィッティング
データフィッティングは、
最適化の一部であると思われない場合も多いようですが、
大抵の場合、上記の数式に当てはめることができ、
最適化問題だとすることができます。
入力として、モデルパラメータを利用し、
データに対する当てはめ誤差を評価関数とすることで、
データフィッティングをすることができます。 制約条件としては、パラメータの制約条件をそのまま利用することが多いようです。
ロボット工学
ロボット工学の分野でも最適化技術は広く利用されます。
例えば、経路生成では、
経路を評価するコスト関数を設定することで、
ロボットにとって走行しやすいコースを生成する手法などに利用されています。
また制御においても、最適化技術を利用するものがあります。
下記の記事で紹介したモデル予測制御という技術で、
入力をロボットの制御値とし、
制約条件をロボットのモデルを利用することで、
ロボットにとって最適な制御を実施する手法もあります。
最適化問題の解き方
一般的に上記の最適化問題を汎用的に解くことは非常に難しいです。
いくつか、手法は提案されていますが、
非常に計算時間がかかってしまったり、
必ずしも答えを得ることができないものが多いようです。
しかし、上記の最適化問題の内、
ある特定の形式の問題は、効率的にかつ安定して解くことができます。
それは下記の5つの場合です。
最小二乗法問題
最小二乗法は、
求めたい入力xに対して、下記のような形で
評価関数を設定できる問題のことを指します。

つまりAx=Bの線形方程式で表される場合です。
上記のようなコスト関数の場合、
最適値は下記のように解析的に求めることができます。

上記のように、解析的に最適化を実現できるので、
最小二乗法を安定的に解くことができる
ソフトウェアは沢山あります。
ちなみにこの最小二乗法の解き方では、
制約条件は一般的に無いことが仮定されています。
制約無し最適化
制約条件が無い場合の最適化の場合、
各パラメータとコスト関数の勾配情報を使って、
コスト関数を逐次的に小さくするように、
パラメータを更新する勾配法と、
勾配情報を使わないシンプレックス法という方法が使われます。
勾配法の場合、最急降下法や
共役勾配法
ニュートン法
順ニュートン法
などが有名です。
上記の勾配法は、手軽に最適化が実現できますが、
初期パラメータに最適化の精度が依存しており、
大域的な最適性を保証してくれないことに注意が必要です。
シンプレックス法の場合、Nelder-Mead法という方法が有名です。
ちなみに、制約条件がある場合でも、
ラグランジュの未定乗数法という手法を使うことで、
制約条件を最適パラメータとして取り込むことで、
上記の方法で解くことができるようになる場合もあります。
線形計画法問題
線形計画法は、
下記の式のように、コスト関数がcxと
線形方程式で表され、
制約条件が等号・不等号式で表せる最適化問題です。

このような線形計画問題は、
先程の最小二乗法のように解析に解くことは出来ませんが、
シンプレックス法という方法を利用することで、
安定して最適値を求める方法が確立されています。
線形計画法の詳細については、
下記の記事を参照下さい。
二次計画法問題
二次計画法は、
先程の線形計画法に似てきますが、
コスト関数が二次式の形式になっている場合に
利用できる最適化技術です。
こちらも、解析的には最適値を計算することができませんが、
逐次的な計算をすることで、
最適化を実現する方法が提案されています。
二次計画法の詳細については、
下記の記事を参照下さい。
凸最適化
凸最適化(Convex Optimization)は、
前述の最適化の定式において、
コスト関数と制約の式が、
下記のような条件を満たす時に、
利用できる最適化手法です。
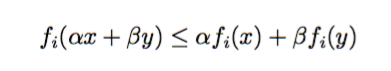
実は、先程の最小二乗法や線形計画法も、
この条件を満たすため、凸最適化の一つであるといえます。
この凸最適化も、
解析に解くことは出来ませんが、
効率的で、精度の高い最適化の技術が提案されています。
また、多くの最適化問題は数式的なトリックを使うことで、
この凸最適化に帰着させることができるのです。
凸最適化の概要に関しては、下記を参照下さい。
最適化ツール群
最適化はかなり複雑な技術ですので、
既存のツールを使うと協力な技術になります。
代表的なものとして、下記が上げられます。
C++製非線形最適化ライブラリCeres Solver
MATLAB製 凸最適化モデリングライブラリ CVX
Python製 凸最適化モデリングライブラリ CVXpy
凸最適化Cコードジェネレータ cvxgen
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。