目次
はじめに
以前、凸最適化技術の基礎として、
線形計画法や、二次計画法の概要を説明し、
凸最適化の有名な応用例である
ナップザック問題を解くシミュレーションを紹介しました。
今回は同じく、凸最適化の応用例として有名な
ポートフォリオ最適化問題の概要と、
ポートフォリオフォリオ最適化問題を解く、
Juliaサンプルコードを紹介したいと思います。
ポートフォリオ最適化問題
ポートフォリオ最適化問題は、
金融工学の有名な問題の一つで、
複数の投資先(アセット)に、
それぞれどれだけ投資すれば良いかという最適化問題です。
このポートフォリオ最適化問題は、
最適化問題の設定によって様々な定式化が可能なのですが、
代表的な最適化の定式化として、
アメリカの経済学者マーコウィッツが提唱した、
Markowitz Portfolioが下記の式です。
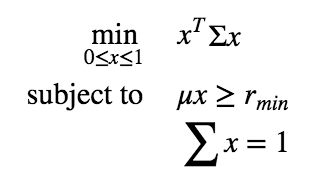
上記の式において、
xは各投資先に対する資産の配分の割合で、
xのそれぞれの要素は0<x_i<1の範囲の値を持ちます。
加えて、xの総和は1になるような制約も加えられます。
一つ目の制約は、
μは各投資先の平均利益率を表したもので、
その平均利益率を資産配分のxでそれぞれ積和をとった値が、
r_min以上になるような制約です。
このr_mimはパラメータで、
すべての資産の平均利益率がある一定値になるように設定できます。
最後に評価関数としては、Σを各資産の時系列データから計算した
共分散行列とし、それとxの二次形式を計算することで
Markowitz Portfolioの評価関数としては、
資産の分散の総和が小さくなるような、
資産配分になるように最適化されます。
線形制約のみのポートフォリオ最適化
先程のMarkwitz Portfolioの最適化の場合は、
線形の不等式制約が入っているため、
解くのが多少難しいですが、
線形制約のみのポートフォリオ最適化の方法もあります。
まず目標となる利益率ρを決定し、
その値以上の利益率になるような不等式制約ではなく、
その値になる等式制約にします。
その状態でポートフォリオの時系列データの平均が、
その利益率にできるだけ近づくようにコスト関数を設定します。
式にすると下記の通りです。

Rはn個の投資先のm時刻分の利益率を格納した行列です。
線形制約の一番上の制約は、投資割合のwの和が1になるようにする制約です。
上記のようなポートフォリオ最適化式の場合、
下記のようにKKT行列の逆数を計算することで、
簡単に最適な投資割合wを計算することができます。

Juliaによるポートフォリオ最大化問題解法サンプルコード
前述のMarkowitz Portfolioの最適化のサンプルコードを
下記のリポジトリで公開しています。
今回は、最適化コードの言語としてJuliaを利用し、
Juliaの最適化ライブラリJuMPも利用しています。
また、上記のリポジトリでは、
JuliaカーネルIJuliaを使って、
Jupyter notebook形式で作成しました。
下記は今回サンプルコードで使用した
3種類の投資先の時系列の利益率データになります。

下記はこのデータをグラフ化したものです。
それぞれの投資先において、
利益率の平均と分散が異なることがわかります。

下記はそれぞれのr_minの値において、
3つの投資先への投資配分をグラフにしたものです。

上記のコードを見ると分かる通り、
r_minの値を変化させると投資先3への投資額は変わりませんが、
投資先1と2の配分が変化していることがわかります。
r_minが上がると、資産の分散よりも
平均利益率が重要視されるため、
分散は大きいが、利益平均値も高い投資先2が重要視されるようです。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
