目次
- 目次
- はじめに
- Position TrackingとTrajectory Estimation
- Graph SLAMとは?
- Ceres Solverを使ったGraph SLAMのサンプルコード
- 参考資料
- MyEnigma Supporters
はじめに
今回も、C++最適化ライブラリCeres Solver関連の記事です。
今回は、Ceres Solverを使って、
移動ロボットで良く利用されるGraph SLAMの
非常にシンプルなサンプルコードを作成してみたいと思います。
Position TrackingとTrajectory Estimation
移動ロボットにおいて、位置推定というと、
現在のセンサの情報から、
リアルタイムに現在のロボットの位置を推定する、
Position Trackingと、
すべてのセンサデータから、
後処理ですべての移動軌跡を推定する、
Trajectory Estimationの2つがあります。
一つ目の手法はカルマンフィルタや
パーティクルフィルタを使ったものが一般的です。
この手法を使うと、リアルタイムでロボットの位置を推定することができるので、
広くロボットの自律移動システムで利用されています.
下記の図はPosition Trackingを図示したものです。
t4の時にランドマークを観測して、位置を補正しています。
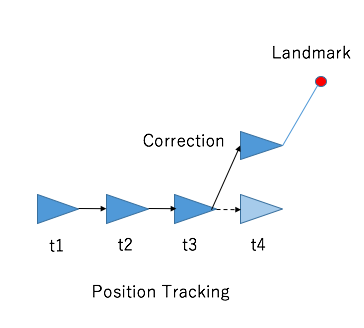
しかし、問題がある場合もあります。
それは、このPosition Trackingの技術では、
あるセンサデータによって、現在の位置は補正できるものの、
過去の軌跡は補正されないのです。
例えば上記の図だと、t4の位置は補正されますが、
t2,t3の時の位置は補正されません。
この問題は、ロボットを使って
精密な地図を作りたい時などに問題になります。
t2とt3の時の位置の精度が悪いので、
その位置を使って地図を作ると地図の精度が劣化してしまうのです。
そんな時に使用されるのがTrajectory Estimationの技術です。
下記の図のように、t4の時の観測値が得られた時点で、
その情報をt2,t3のデータにフィールドバックすることで、
現在の位置だけでなく、軌跡すべてを補正します。

このTrajectory Estimationは、
一回の観測ですべての軌跡を補正するため、
膨大な計算になることが多いため、
一般的にはすべてのデータを取得したあと、
後処理として実行することが多いようです。
Graph SLAMとは?
Graph SLAMは、
上記のTrajcetory Estimationに利用される技術の一つです。
(Trajectory Estimationだけでなく、SLAMという名前にもある通り、
地図構築にも利用されます
Graph SLAMは、グラフ理論の考えを使って、
下記の図のように、各状態量をエッジとノードで繋ぎ、
そのエッジのコストを最小するような最適化を実施することにより、
Trajectory Estimationを実施したり、
地図構築を実施します。

Graph SLAMの詳細については、
下記の資料を参照下さい。
Ceres Solverを使ったGraph SLAMのサンプルコード
今回は、非常にシンプルな、
Graph SLAMのサンプルとして、
オドメトリとデータ取得周期の長いGPSを備え付けたロボットの
Trajectory Estimationを考えます。
まず下記のpythonコードで、
オドメトリとGPSのデータを擬似的に生成しました。
#!/usr/bin/env python # -*- coding: utf-8 -*- u""" Data generator for 2D Trajectory optimization auther: Atsushi Sakai """ import matplotlib.pyplot as plt import numpy as np import math import pandas as pd def MotionModel(x,u,dt): x[0]=x[0]+u[0]*dt*math.cos(x[2]) x[1]=x[1]+u[0]*dt*math.sin(x[2]) x[2]=x[2]+u[1]*dt return x def AddInputNoise(u,Q): un=u[:] un[0]=un[0]+np.random.randn()*Q[0] un[1]=un[1]+np.random.randn()*Q[1] return un def Observation(xTrue,R,time,zdt): z=[0,0,0] if abs(time%zdt) > 0.1: return z z[0]=xTrue[0]+np.random.randn()*R[0] z[1]=xTrue[1]+np.random.randn()*R[0] z[2]=R[0] return z xTrue=[0,0,0]# state x,y,yaw x=[0,0,0]# state x,y,yaw u=[1.0,0.1]# input v[m/s],omega[rad/s] Q=[0.5,0.1] #input noise R=[0.1] #observation noise z=[0,0]# state x,y,yaw dt=0.1 #[s] zdt=4.0 #[s] time=0.0 SimTime=50.0 true_x = [] true_y = [] true_yaw = [] odo_x = [] odo_y = [] odo_yaw = [] z_x = [] z_y = [] z_n = [] u_dl = [] u_dtheta = [] u_dl_n = [] u_dtheta_n = [] plt.grid(True) plt.axis("equal") while time<SimTime: time+=dt xTrue=MotionModel(xTrue,u,dt) un=AddInputNoise(u,Q) x=MotionModel(x,un,dt) z=Observation(xTrue,R,time,zdt) # data store true_x.append(xTrue[0]) true_y.append(xTrue[1]) true_yaw.append(xTrue[2]) odo_x.append(x[0]) odo_y.append(x[1]) odo_yaw.append(x[2]) z_x.append(z[0]) z_y.append(z[1]) z_n.append(z[2]) u_dl.append(un[0]*dt) u_dtheta.append(un[1]*dt) u_dl_n.append(Q[0]*dt) u_dtheta_n.append(Q[1]*dt) # show figure plt.plot(true_x,true_y,"-b",label="True"); plt.plot(odo_x,odo_y,"-r",label="odometry"); plt.plot(z_x,z_y,"xg",label="GPS"); plt.legend() plt.show() # save csv df=pd.DataFrame() df["true_x"] = true_x df["true_y"] = true_y df["true_yaw"] = true_yaw df["odo_x"] = odo_x df["odo_y"] = odo_y df["odo_yaw"] = odo_yaw df["z_x"] = z_x df["z_y"] = z_y df["u_dl"] = u_dl df["u_dtheta"] = u_dtheta df["z_n"] = z_n df["u_dl_n"] = u_dl_n df["u_dtheta_n"] = u_dtheta_n df.to_csv("data.csv")
上記のコードで、
生成されたデータを元に、
オドメトリのデータ(並進移動量と方位変化量)と
GPSのデータ(x,y)を使って出来るだけ精度の良い
走行軌跡を生成したいと思います。
(両方のセンサデータにはノイズが負荷されています。)
まず、Graph SLAMのエッジとして、
二種類のエッジを定義します。
一つはOdometry Constraintです。
ある地点の位置をその時のオドメトリデータで更新し、
その位置が次の位置に出来るだけ近くなるようにします。
今回のコスト関数はセンサの事前誤差量を使って、
マハラノビス距離を計算することで、その値をコストとしました。
コスト項としては、下記のようになります。

このコストを最小化することで、
できるだけオドメトリデータを信じるようになります。
Ceresのコードとしては、下記のように評価関数を作りました。
基本的には以前紹介したCeresのサンプルコードと同じ感じです。
struct OdometryConstraint{ OdometryConstraint(double dl, double dtheta, double dl_n, double dtheta_n) :dl_(dl), dtheta_(dtheta), dl_n_(dl_n), dtheta_n_(dtheta_n) {} template <typename T> bool operator()( const T* const cx, const T* const cy, const T* const cyaw, const T* const nx, const T* const ny, const T* const nyaw, T* residual) const { residual[0]=(nx[0]-(cx[0]+dl_*cos(cyaw[0])))/dl_n_; residual[1]=(ny[0]-(cy[0]+dl_*sin(cyaw[0])))/dl_n_; residual[2]=(nyaw[0]-(cyaw[0]+dtheta_))/dtheta_n_; return true; } static ceres::CostFunction* Create( const double dl, const double dtheta, const double dl_n, const double dtheta_n ){ return (new ceres::AutoDiffCostFunction<OdometryConstraint,3,1,1,1,1,1,1>( new OdometryConstraint(dl,dtheta,dl_n, dtheta_n))); } private: const double dl_;//move distance const double dtheta_;//change angle const double dl_n_;// move distance accuracy const double dtheta_n_;// change angle accuracy };
2つ目のエッジはGPS Constraintです。
これはより簡単で、
GPSの観測値と現在の位置ができるだけ近くなるようにするコスト項です。
式としては、下記のようになります。

このコストを最小化することで、
できるだけGPSのデータを信じるようになります。
こちらも下記のようにコスト関数を実装しました。
struct GPSConstraint{ GPSConstraint(double x, double y, double n) :x_(x), y_(y), n_(n) {} template <typename T> bool operator()( const T* const x, const T* const y, T* residual) const { residual[0]=(x[0]-T(x_))/n_; residual[1]=(y[0]-T(y_))/n_; return true; } static ceres::CostFunction* Create( const double gx, const double gy, const double gn ){ return (new ceres::AutoDiffCostFunction<GPSConstraint,2,1,1>( new GPSConstraint(gx,gy,gn))); } private: const double x_;//gps position x const double y_;//gps position y const double n_;//gps xy accuracy };
あとは下記のコードのように、各コスト項を追加して、
最適化を実施するだけです。
上記の2つのコストの和を最小化すると、
オドメトリとGPSの両方を加味した、
最適な軌跡が得られます。
下記が最適化部分のコードです。
下記のコードを見ると分かる通り、
オドメトリのコストは毎回追加していますが、
GPSのコストはデータが取得出来た時のみ追加しています。
//====Optimization===== ceres::Problem problem; for(int i=0;i<csvparser.ncol_-1;i++){ // odometry constraint problem.AddResidualBlock( OdometryConstraint::Create(dl[i],dtheta[i],dl_n[i],dtheta_n[i]), NULL, &(x[i]), &(y[i]), &(yaw[i]), &(x[i+1]), &(y[i+1]), &(yaw[i+1]) ); //gps constraint if(fabs(zn[i])>=0.001){ problem.AddResidualBlock( GPSConstraint::Create(zx[i],zy[i],zn[i]), NULL, &x[i], &y[i] ); } } //Optimization Solver::Options options; options.linear_solver_type=ceres::DENSE_QR; options.minimizer_progress_to_stdout=true; Solver::Summary summary; Solve(options,&problem,&summary);
このコードを実行結果は下記の通りです。
ちゃんとコストが徐々に小さくなり、
4回のイタレーションで収束しています。
(自分のMacbook上のVMで約10秒計算がかかりました)

下記が結果のグラフです。

青線が真のロボットの軌跡、
緑線がオドメトリの軌跡(ノイズにより精度が低下)
黒バツがGPSの位置(精度は良いですが、データの取得が遅い)
そして、赤線が最適化後の軌跡になります。
この赤線の結果を見ると分かる通り、
オドメトリとGPSのデータを使って、
軌跡全体が真の軌跡に近づき、
高精度に推定出来ていることがわかります。
(カルマンフィルタなどを使った場合は、
GPSが取得された点以外は補正されません)
以上のコードはすべて下記で公開されています。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
