作者: 金谷健一
出版社/メーカー: 共立出版
発売日: 2005/09/01
メディア: 単行本
購入: 29人クリック: 424回
この商品を含むブログ (41件) を見る

Ceres Solverとは？

Ceres Solverは、

Googleが開発＆公開している

オープンソースの最適化用C++ライブラリです。

複雑で大規模な最適化問題をモデリングしたり、

解いたりすることができます。

このCeres Solverは2010年からGoogleの製品にも使われてきました。

Ceres Solverは下記の二つの用途で使用することができます。

制約付き非線形最小二乗問題
制約なしの最適化問題

今回の記事ではこのCeres Solverのインストール方法から

Ceres Solverを使用したサンプルコードまで説明したいと思います。

Ceresの名前の由来

Ceresは、準惑星の1つなのですが、

ケレス (準惑星) - Wikipedia

ガウスが最小二乗法を使って軌道計算したことにより、

発見された準惑星です。

Ceresは最小二乗法による初めての大きな発見であるため、

この非線形系最適化のライブラリも

Ceresという名前になったとのことです。

Ceres Solverの特徴

Ceres Solverは下記のような特徴を有しています。

シンプルでわかりやすいAPI
自動微分機能
ロバストな損失関数
スレッド化されたヤコビアン評価機能と線形ソルバー
小規模システムのための密QR分解
大規模システムのための疎コレスキー分解
三次元画像処理のためのソルバー
使いやすいライセンス (New BSD)
スマートフォンからサーバまで利用可能

Ceres Solverの利用用途

Street View sensor fusion with Ceres Solver

各プラットフォームのインストール方法

Ceres SolverはLinux,Mac,Windows,Android,iOSで利用できます。

各プラットフォームにおけるインストールは、

下記の公式ドキュメントがわかりやすいです。

Building & Installation — Ceres Solver

Ceres Solverを使った最適化サンプルコード

Ceres Solverを使ったサンプルコードに関して説明します。

サンプルの最適化処理を実行する

マニュアルに書かれているように、

binの下にあるsimple_bundle_adjusterを実行することで、

バンドル調整を実施することができます。

$ bin/simple_bundle_adjuster ../ceres-solver-1.11.0/data/problem-16-22106-pre.txt

すると標準出力に下記のように処理結果が表示されるはずです。

f:id:meison_amsl:20160921133221p:plain

f:id:meison_amsl:20160921133229p:plain

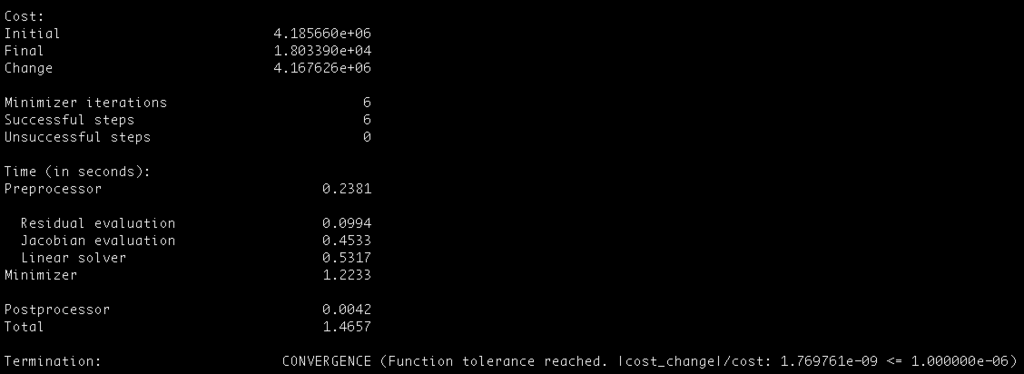
どのような処理が実施されたのか、よくわからないですが、

とりあえず最適化が成功したようです。

あとは、自分が解きたい問題を

上記のように解けるようにCeresを設定すれば良いということになります。

制約付き非線形最適化の基礎

Ceresは下記の式で表すことができる

制約付き非線形最小二乗問題を解くことができます。

f:id:meison_amsl:20160921134209p:plain

このような制約付き非線形最小二乗問題は、

統計学におけるフィッティングや、

myenigma.hatenablog.com

画像群による３次元復元、

そして最新制御技術などの

myenigma.hatenablog.com

様々な科学・工学分野で利用されます。

上記の式における

f:id:meison_amsl:20160921134934p:plain

の部分は残差項と呼ばれ、

関数fはコスト関数と呼ばれます。

コスト関数fは

パラメータ項[xi1,xi2,xi3,xi4,...]によって計算されます。

多くの最適化問題は、

それぞれのパラメータ群をまとめてパラメータ項にすることで

上記の問題に帰着することができます。

例えば、カメラの位置を最適化問題で解く場合は、

三次元位置のパラメータ３つと

クォータニオンのパラメータ４つを

まとめてパラメータ項にすることで、

上記の式に帰着することができます。

また、それぞれのパラメータには制約条件を設定出来る場合があります。

例えば、あらかじめカメラの位置がわかる場合や、

カメラのオイラー角のパラメータの場合は-180度〜180度など、

がパラメータ項の制約条件です。

これを設定することで、制約条件の中で最適化問題を解くことができ、

より精密な解を得ることができるようになります。

上記の式においては、

f:id:meison_amsl:20160921140018p:plain

が制約条件の項になります。

lが下限制約、uが上限制約です。

ρiは損失関数と呼ばれ、

スカラー関数として設定されます。

この損失関数は、非線形最適化において、

外れ値の影響をできるだけ小さくするために、

利用されます。

また、損失関数をすべて1とし、

制約条件を設定しない場合は、

下記の式のようなシンプルな形にすることもできます。

f:id:meison_amsl:20160921140420p:plain

非常に簡単な非線形最適問題を解いてみる

Ceresソルバの使い方の説明として、

非常にシンプルな非線形最適化問題を実際に問いてみたいと思います。

下記の式の最小値を取得したいとします。

f:id:meison_amsl:20160922024811p:plain

Ceresを使わずとも、最小値はx=10であることはわかりますが、

例題としてCeresで解いてみます。

まず初めにやることは、評価関数の導関数を設定することです。

上記の式では、f(x)=10-xになります。

上記の導関数を設定する場合、

下記のように導関数用の構造体を設定します。

struct CostFunctor{
    template <typename T>
    bool operator()(const T* const x, T* residual) const{
        residual[0]=T(10.0)-x[0];
        return true;
        }
};

ここで、Ceresではtemplateを使って、

導関数の入力と出力を設定します。

Ceresの場合は入力と出力の型が同じである必要があります。

この例の場合は両方とも型Tはdoubleですが、

ヤコビ行列などを設定することもできるようです。

加えて、Ceresのソルバーは、

CostFunctor::operator()という関数を

コスト関数として認識するようになっています。

続いて、実際にこの評価関数を使って、

最適化問題を解くコードを書きます。

/**
 *  @brief Ceres Optimimization Sample
 *
 *  @author Atsushi Sakai
 *
 **/

#include "ceres/ceres.h"
#include "glog/logging.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

/**
 *  @brief コスト関数
 **/
struct CostFunctor{
    template <typename T>
    bool operator()(const T* const x, T* residual) const{
        residual[0]=T(10.0)-x[0];
        return true;
        }
};


int main(int argc, char** argv){
  google::InitGoogleLogging(argv[0]);

  //最適化問題を解く変数と初期値の設定
  double initial_x=5.0;
  double x=initial_x;

  //最適化問題を解く用のオブジェクトの生成
  Problem problem;

  //コスト関数の設定
  //AutoDiffCostFunctionを使うことで、自動的にヤコビ行列を設定できる
  CostFunction* cost_function=new AutoDiffCostFunction<CostFunctor,1,1>(new CostFunctor);

  //最適化問題に残差項と変数を設定
  problem.AddResidualBlock(cost_function,NULL,&x);

  //最適化の実行
  Solver::Options options;//最適化のオプション設定用構造体
  options.linear_solver_type=ceres::DENSE_QR;
  options.minimizer_progress_to_stdout=true;//最適化の結果を標準出力に表示する。
  Solver::Summary summary;//最適化の結果を格納するよう構造体
  Solve(options,&problem,&summary);//最適化の実行

  //結果の表示
  std::cout<<summary.BriefReport()<<std::endl;
  std::cout<<"x:"<<initial_x<<"->"<<x<<std::endl;

  return 0;
}