
Vehicle Dynamics and Control (Mechanical Engineering Series) (English Edition)
目次
- 目次
- はじめに
- 自動車の代表的なステアリングモデル
- 2つのモデルの軌跡比較
- 直線コースにおけるBicycle Modelの線形ステアリングモデル
- 目標コース座標系における線形Dynamic Bicycle Model
- 車両の進行方向モデル
- より詳しく学びたい方は
- 参考資料
- MyEnigma Supporters
はじめに
以前、
車両ダイナミクスの基礎という記事を書きましたが、
今回は自動車制御のための、
様々な車両モデリングの方法と
その特徴について説明したいと思います。
自動車の代表的なステアリングモデル
まず初めに自動車の代表的な2つのモデルについて述べます。
Kinematic Model
Kinematic Modelは、力学的な関係による車両モデルで、
車両中心をどこに置くかによって、式が変わります。
後輪の真ん中を中心とした場合、
Unicycle Modelと呼ばれることが多いです。

Unicycle Modelは非常にシンプルなモデルです。
後輪中心からL (上記の図ではr)離れたステアリングを切ることで、
車両方位が変わり、その方位と車速から位置を更新します。
下記がUnicycle Modelの式です。

以前紹介したパスプランニングアルゴリズムである、
Dubinsパスもこのモデルをベースにしています。
車両の重心を中心とした場合、
下記の図のように車両のすべり角を考慮します。

上記のモデルの場合、
ステアリングを切った場合、
前輪と後輪の速度ベクトルがそれぞれ別々の車輪の方向を向くので、
それらを組み合わせた、車両中心の速度ベクトルは、
車両の方向とは一致しなくなります。
そのような状態を力学的(幾何学的)にモデリングしたので、
式は下記のようになります。

上記のKinematic Bicycle modelは、
それぞれの車輪のすべり角は考慮していないため、
車輪のすべり角が大きくなる高速域では、
精度が低下してしまいます。
一般的に、速度が20km/h以下ぐらいの場合は、
Kinematic Bicycle Modelで十分精度が出るようで、
自動駐車などの制御ではKinematic Bicycle Modelが使用されています。
Dynamic Bicycle Model

Kinematic Modelは、
力学的(幾何学的)な関係から導き出されたモデルですので、
高速域で精度が低下してしまいます。
そこで、より精度が高いモデルとして使用されるのが、
Dynamic Bicycle Modelです。
下記の記事で説明した、
すべり角とタイヤの力学から、
コーナリングフォースを規定し、
それらの情報から、運動方程式を使って、
モデルを構築します。
下記がDynamic Bicycle Modelの更新式です。

Dynamic Bicycle Modelは
非常に精度の高いモデルですが、
タイヤのコーナリングスティフネスや、
精密な重心位置などがわかる必要があるため、
パラメータの同定が大変だったり、
式が複雑で計算コストが高いという問題があります。
また式を見ると分かる通り、
分母にvxが入っているため、
速度が0の時に計算が出来なくなるという問題があります。
2つのモデルの軌跡比較
上記の2つのモデルを使用し、
同じ入力を入れた時の軌跡を比較してみました。
比較のコードはこちらにあります
下記の図は軌跡の比較のグラフです。

Kinematic modelとDynamic Modelを比較すると、
車両のパラメータによって、
軌跡に差が生まれていることがわかります。
直線コースにおけるBicycle Modelの線形ステアリングモデル
下記の記事のBicycle Modelは非線形の運動モデルですが、
微少角度の近似と高次元項を無視することで、
線形モデル化することができます。
もし、前進速度を状態ベクトルに入れてしまうと、
車両モデルは非線形になってしまうので、
車両モデルを線形するために、
前進速度は定速仮定を置きます。
(制御ループ毎にモデルを更新すれば近似誤差を抑えることができます。)
また、タイヤの挙動も線形であることを仮定します。
(タイヤのモデルに関しては下記を参照下さい)
横方向の運動方程式は下記になり、

回転方向の運動方程式は下記になります。
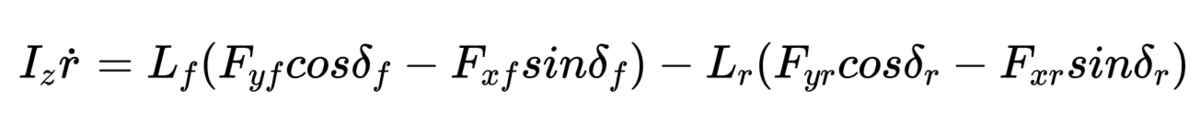
ここで、定速仮定と前後方向の空力などの力は小さいと仮定すると、
Fxf=Fxr=0とすることができ、
またステアリング角度が小さいとすると、
cosδ=1, sinδ=δと近似できるので、
上記の二式は下記になります。

続いて、前後輪線形タイヤモデルと

すべり角αの定義を使って、
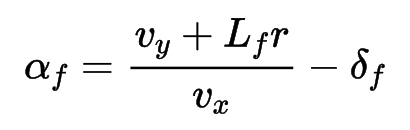
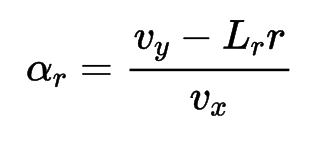
全後輪のすべり角を消去して、
先ほどの式に入れると下記のような
線形モデルを作ることができます。
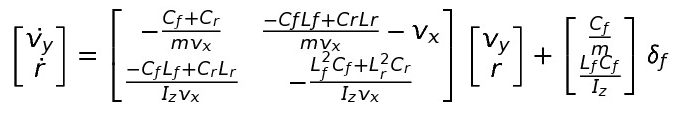
上記の式を離散の差分方程式になると下記のようになります。
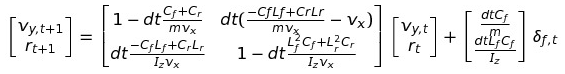
また、VとV_dot, φとφ_dotの4つを状態ベクトルに入れた場合、
下記のようになります。
(コーナリングパワーが一輪のものになっていることに注意)

上記のような車両モデルの線形化は、
下記のような制御ロジックを使うために利用されます。
目標コース座標系における線形Dynamic Bicycle Model
前述のDynamic Bicycle Modelの線形モデルを使うと、
ある目標コース座標系における、
横方向と旋回方向の線形モデルを構築することができます。
これは、目標コースが直線だけでなく、
ある旋回半径Rを保つ場合でも対応できます。
現在の目標コースをR、前進速度をVxとすると、
その時の旋回速度は下記の式で表現されます。
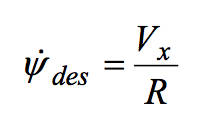
すると、線形化されたBicycle Modelは、
下記のようになります。


また、上記のモデルからグローバル座標系での
X,Y座標値は下記の積分計算で計算できます。

このモデルは、自動車の自動レーンキービングコントローラなどに
よく使われます。
車両の進行方向モデル
上記は車両に対して横方向に影響を与える
ステアリングモデルでしたが、
続いて車両の進行モデルについて述べます。
車両の進行方向に対する運動方程式は下記になります。


上記において、
左側は車両重量mと進行方向の加速度です。
右側は車両の進行方向に影響を与える力であり、
下記の種類の力がかかります。
Fxf: 前輪の駆動力
Fxr: 後輪の駆動力
Faero: 空気抵抗力
Rxf: 前輪転がり抵抗
Rxr: 後輪転がり抵抗
mgsin(θ): 傾斜による重力
続いて、上記の力について説明します。
空気抵抗
空気抵抗力は下記から計算されます。

ρは空気密度
Cdは空気抵抗定数
Afは有効面積
Vxは車両速度
Vwindは風速です。
上記の式を見ると分かる通り、
空気抵抗力は速度の二乗に比例して大きくなります。
タイヤの推進力
前輪後輪の推進力は下記の式で計算できます。

Cは前輪後輪の推進力定数、
σは前輪後輪のスリップ率です。
下記で説明している通り、
タイヤの等方性という考えを使うことで、
横方向のコーナリングフォースも、
推進力も同じように滑り量で線形で増えるモデルが使われています。
転がり抵抗力
前輪後輪の転がり抵抗力は下記の式で計算されます。

上記の式において、
fは転がり抵抗力係数、
FzfとFzrは前輪と後輪の垂直抗力です。
上記の式のように、
転がり抵抗力は、前輪後輪の垂直抗力の和に比例します。
fは転がり抵抗力係数fは乗用車では、
0.001から0.04ほどの値を取るようです。
より詳しく学びたい方は
上記の車両のモデリングに関しては、
下記の書籍をベースにまとめました。
上記のモデリングを、
一から導出しており、
非常にわかりやすい書籍ですのでおすすめです。
参考資料

Vehicle Dynamics and Control (Mechanical Engineering Series) (English Edition)
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
