目次
はじめに
以前、移動ロボットにおける
パスプランニングアルゴリズムとして、
Dynamic Window Approachや、
ダイクストラ法,
A*法
Rapidly-Exporing Random Trees
などのアルゴリズムとサンプルコードを紹介しましたが、
今回は、Dubins Pathという非常に古典的でありながら、
シンプルなアプリケーションでは、
未だによく使われるパスプランニングの技術を紹介し、
シンプルなPythonサンプルコードを紹介したいと思います。
Dubins Pathとは?
Dubinsパスとは、
1957年にDubinsによって提案されたコース生成手法です。
スタート地点とゴール地点の(x,y,yaw)と、
旋回曲率を与えることで、
2つの旋回コースと直線を使って、
スタート地点から、ゴール地点までの最短コースを生成することができます。
このDubinsパスは非常にシンプルでありながら、
理論的に最短コースを生成できるため、
車両型のロボットや、海中ロボット、
飛行ロボットのコース生成などによく使用されるようです。
Dubins Pathの概念
Dubinsパスは、
二次元空間上の2つの位置(x,y)と姿勢(yaw)、
そして旋回コースの旋回半径を与えると、
二点間の理論的最短のパスを生成してくれます。
しかし、車両は前進のみするという条件があります。
Dubinsのパスでは、下記の図のように、
二点間のパスを3つの部分に分け、
それらの部分がそれぞれ右旋回、左旋回、直線の
いずれかで表されるとしています。


ここで、右旋回をR, 左旋回をL, 直線をSとします。
すると、上記の一つ目のコースはRSL,
二つ目のコースはRSRのようにカテゴライズできます。
Dubinsの功績は、
上記の二点2D状態量を結ぶ最短コースは、
下記の6つのコースカテゴリのいずれかになるということを
理論的に証明したことです。
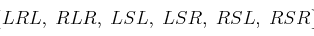
また、それぞれのコース形状は、
幾何学的関係から非常に簡単に計算することができます。
参照: Classification of the Dubins set
下記の図は、ある二点2D状態量(2つの矢印)を結ぶ
それぞれのコースを計算したものです。
6種類コースがあるのですが、
下記の条件だと2つのコースが生成出来なかったため、
4つのパスが生成されています。

Dubinsパスでは、上記の6本のコースを生成し、
その中から最もパスの長さが短いコースを最短コースとします。
前述の通り、このコースは円と直線で構成されたコースとしては、
理論的に最短になることが知られています。
Pythonサンプルコード
下記がPythonサンプルコードです。
mainの部分を見てもらえると分かる通り、
startとendの状態量と旋回半径を与えると、
最短コースが返ってきます。
#! /usr/bin/python # -*- coding: utf-8 -*- """ Dubins path planner sample code author Atsushi Sakai(@Atsushi_twi) License MIT """ import math def mod2pi(theta): return theta - 2.0 * math.pi * math.floor(theta / 2.0 / math.pi) def pi_2_pi(angle): while(angle >= math.pi): angle = angle - 2.0 * math.pi while(angle <= -math.pi): angle = angle + 2.0 * math.pi return angle def LSL(alpha, beta, d): sa = math.sin(alpha) sb = math.sin(beta) ca = math.cos(alpha) cb = math.cos(beta) c_ab = math.cos(alpha - beta) tmp0 = d + sa - sb mode = ["L", "S", "L"] p_squared = 2 + (d * d) - (2 * c_ab) + (2 * d * (sa - sb)) if p_squared < 0: return None, None, None, mode tmp1 = math.atan2((cb - ca), tmp0) t = mod2pi(-alpha + tmp1) p = math.sqrt(p_squared) q = mod2pi(beta - tmp1) # print(math.degrees(t), p, math.degrees(q)) return t, p, q, mode def RSR(alpha, beta, d): sa = math.sin(alpha) sb = math.sin(beta) ca = math.cos(alpha) cb = math.cos(beta) c_ab = math.cos(alpha - beta) tmp0 = d - sa + sb mode = ["R", "S", "R"] p_squared = 2 + (d * d) - (2 * c_ab) + (2 * d * (sb - sa)) if p_squared < 0: return None, None, None, mode tmp1 = math.atan2((ca - cb), tmp0) t = mod2pi(alpha - tmp1) p = math.sqrt(p_squared) q = mod2pi(-beta + tmp1) return t, p, q, mode def LSR(alpha, beta, d): sa = math.sin(alpha) sb = math.sin(beta) ca = math.cos(alpha) cb = math.cos(beta) c_ab = math.cos(alpha - beta) p_squared = -2 + (d * d) + (2 * c_ab) + (2 * d * (sa + sb)) mode = ["L", "S", "R"] if p_squared < 0: return None, None, None, mode p = math.sqrt(p_squared) tmp2 = math.atan2((-ca - cb), (d + sa + sb)) - math.atan2(-2.0, p) t = mod2pi(-alpha + tmp2) q = mod2pi(-mod2pi(beta) + tmp2) return t, p, q, mode def RSL(alpha, beta, d): sa = math.sin(alpha) sb = math.sin(beta) ca = math.cos(alpha) cb = math.cos(beta) c_ab = math.cos(alpha - beta) p_squared = (d * d) - 2 + (2 * c_ab) - (2 * d * (sa + sb)) mode = ["R", "S", "L"] if p_squared < 0: return None, None, None, mode p = math.sqrt(p_squared) tmp2 = math.atan2((ca + cb), (d - sa - sb)) - math.atan2(2.0, p) t = mod2pi(alpha - tmp2) q = mod2pi(beta - tmp2) return t, p, q, mode def RLR(alpha, beta, d): sa = math.sin(alpha) sb = math.sin(beta) ca = math.cos(alpha) cb = math.cos(beta) c_ab = math.cos(alpha - beta) mode = ["R", "L", "R"] tmp_rlr = (6.0 - d * d + 2.0 * c_ab + 2.0 * d * (sa - sb)) / 8.0 if abs(tmp_rlr) > 1.0: return None, None, None, mode p = mod2pi(2 * math.pi - math.acos(tmp_rlr)) t = mod2pi(alpha - math.atan2(ca - cb, d - sa + sb) + mod2pi(p / 2.0)) q = mod2pi(alpha - beta - t + mod2pi(p)) return t, p, q, mode def LRL(alpha, beta, d): sa = math.sin(alpha) sb = math.sin(beta) ca = math.cos(alpha) cb = math.cos(beta) c_ab = math.cos(alpha - beta) mode = ["L", "R", "L"] tmp_lrl = (6. - d * d + 2 * c_ab + 2 * d * (- sa + sb)) / 8. if abs(tmp_lrl) > 1: return None, None, None, mode p = mod2pi(2 * math.pi - math.acos(tmp_lrl)) t = mod2pi(-alpha - math.atan2(ca - cb, d + sa - sb) + p / 2.) q = mod2pi(mod2pi(beta) - alpha - t + mod2pi(p)) return t, p, q, mode def dubins_path_planning_from_origin(ex, ey, eyaw, c): # nomalize dx = ex dy = ey D = math.sqrt(dx ** 2.0 + dy ** 2.0) d = D / c # print(dx, dy, D, d) theta = mod2pi(math.atan2(dy, dx)) alpha = mod2pi(- theta) beta = mod2pi(eyaw - theta) # print(theta, alpha, beta, d) planners = [LSL, RSR, LSR, RSL, RLR, LRL] bcost = float("inf") bt, bp, bq, bmode = None, None, None, None for planner in planners: t, p, q, mode = planner(alpha, beta, d) if t is None: # print("".join(mode) + " cannot generate path") continue cost = (abs(t) + abs(p) + abs(q)) if bcost > cost: bt, bp, bq, bmode = t, p, q, mode bcost = cost # print(bmode) px, py, pyaw = generate_course([bt, bp, bq], bmode, c) return px, py, pyaw, bmode, bcost def dubins_path_planning(sx, sy, syaw, ex, ey, eyaw, c): """ Dubins path plannner input: sx x position of start point [m] sy y position of start point [m] syaw yaw angle of start point [rad] ex x position of end point [m] ey y position of end point [m] eyaw yaw angle of end point [rad] c curvature [1/m] output: px py pyaw mode """ ex = ex - sx ey = ey - sy lex = math.cos(syaw) * ex + math.sin(syaw) * ey ley = - math.sin(syaw) * ex + math.cos(syaw) * ey leyaw = eyaw - syaw lpx, lpy, lpyaw, mode, clen = dubins_path_planning_from_origin( lex, ley, leyaw, c) px = [math.cos(-syaw) * x + math.sin(-syaw) * y + sx for x, y in zip(lpx, lpy)] py = [- math.sin(-syaw) * x + math.cos(-syaw) * y + sy for x, y in zip(lpx, lpy)] pyaw = [pi_2_pi(iyaw + syaw) for iyaw in lpyaw] # print(syaw) # pyaw = lpyaw # plt.plot(pyaw, "-r") # plt.plot(lpyaw, "-b") # plt.plot(eyaw, "*r") # plt.plot(syaw, "*b") # plt.show() return px, py, pyaw, mode, clen def generate_course(length, mode, c): px = [0.0] py = [0.0] pyaw = [0.0] for m, l in zip(mode, length): pd = 0.0 if m is "S": d = 1.0 / c else: # turning couse d = math.radians(3.0) while pd < abs(l - d): # print(pd, l) px.append(px[-1] + d * c * math.cos(pyaw[-1])) py.append(py[-1] + d * c * math.sin(pyaw[-1])) if m is "L": # left turn pyaw.append(pyaw[-1] + d) elif m is "S": # Straight pyaw.append(pyaw[-1]) elif m is "R": # right turn pyaw.append(pyaw[-1] - d) pd += d else: d = l - pd px.append(px[-1] + d * c * math.cos(pyaw[-1])) py.append(py[-1] + d * c * math.sin(pyaw[-1])) if m is "L": # left turn pyaw.append(pyaw[-1] + d) elif m is "S": # Straight pyaw.append(pyaw[-1]) elif m is "R": # right turn pyaw.append(pyaw[-1] - d) pd += d return px, py, pyaw def plot_arrow(x, y, yaw, length=1.0, width=0.5, fc="r", ec="k"): u""" Plot arrow """ import matplotlib.pyplot as plt if not isinstance(x, float): for (ix, iy, iyaw) in zip(x, y, yaw): plot_arrow(ix, iy, iyaw) else: plt.arrow(x, y, length * math.cos(yaw), length * math.sin(yaw), fc=fc, ec=ec, head_width=width, head_length=width) plt.plot(x, y) if __name__ == '__main__': print("Dubins path planner sample start!!") import matplotlib.pyplot as plt start_x = 1.0 # [m] start_y = 1.0 # [m] start_yaw = math.radians(45.0) # [rad] end_x = -3.0 # [m] end_y = -3.0 # [m] end_yaw = math.radians(-45.0) # [rad] curvature = 1.0 px, py, pyaw, mode, clen = dubins_path_planning(start_x, start_y, start_yaw, end_x, end_y, end_yaw, curvature) plt.plot(px, py, label="final course " + "".join(mode)) # plotting plot_arrow(start_x, start_y, start_yaw) plot_arrow(end_x, end_y, end_yaw) # for (ix, iy, iyaw) in zip(px, py, pyaw): # plot_arrow(ix, iy, iyaw, fc="b") plt.legend() plt.grid(True) plt.axis("equal") plt.show()
上記のコードは下記でも公開しています。
下記は上記のサンプルコードの処理結果です。


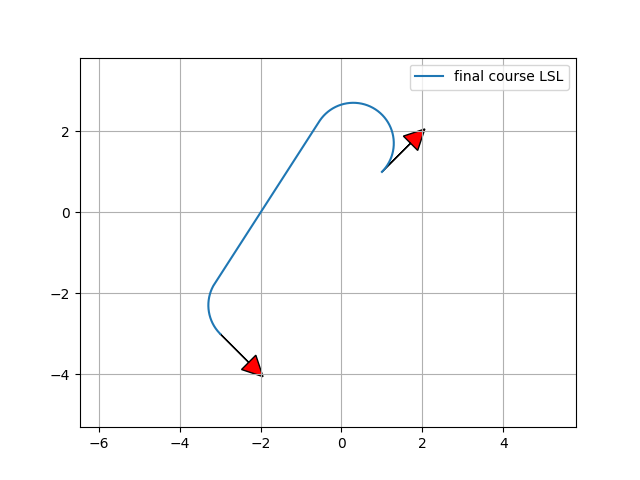
上記の結果を見ると分かる通り、
二次元空間上の二点と旋回半径を指定すると、
最短コースができていることがわかります。
Dubinsパスのその他の使い道
Dubinsパスは上記のようなコース生成以外にも、
二点の2D状態量を評価するのに使用されることがあります。
Dubinsコースの最適コースの長さをDubins metricといい、
RRTなどのサンプリングベースのパスプランニングアプローチの
評価関数として使用することが多いようです。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
