目次
はじめに
これまで、最適化問題の代表的な問題である
ポートフォリオ最適化や、
ナップサック問題問題などを
最適化ライブラリで解く方法を紹介してきましたが、
今回は最大流問題(Max Flow Problem)という
こちらも有名な最適化問題の概要と、
それをプログラムで解く方法について紹介したいと思います。
最大流問題(Max Flow Problem)
最大流問題(Max Flow Problem)は、
代表的な最適化問題の一つです。
各エッジの最大流量が指定された有効グラフの中で
スタートからゴールまで最流量が大きくなるような
各エッジの流量を求める問題です。
例えば、下記のような有効グラフにおいて、
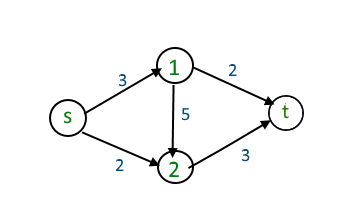
sからtまで最も流量が大きくなる流量を計算する問題です。
この最大流量問題は、
線形計画問題であるため、
大規模なノードの問題でも高速に最適値を計算することができます。
この最大流量最適化は、
ネットワークの最適化に使用されたり、
リソースの最適配分などに利用されます。
Juliaによるサンプルプログラム
今回は、以前紹介したJuliaという言語と、
最適化ライブラリJuMPを使って、
最大流問題を解いてみることにします。
今回は下記のような、
有効グラフにおいて、ノード0からノード5までの
流量が最も大きくなる各エッジの流量を求めたいと思います。
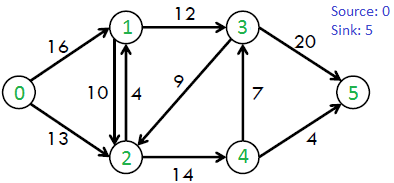
下記がサンプルプログラムです。
基本的には、
各エッジの流量を変数とし、
正の値であることと、
各エッジの最大流量の制約を追加します。
そして、スタートノード(0)とゴールノード(5)以外の
ノード(1-4)の流入と流出は収支が合う必要があるため、
流入と流出の等号制約を追加します。
あとはそれを解くだけです。
前述の通り、最大流量問題は線形計画問題なので、
Clpソルバーで解くことができます。
COIN-OR Linear Programming Solver
# # max flow problem optimization # # author: Atsushi Sakai # using JuMP using Clp solver = ClpSolver() function main() println(PROGRAM_FILE," start!!") model = Model(solver=solver) @variable(model, 0<=x01<=16) @variable(model, 0<=x02<=13) @variable(model, 0<=x12<=10) @variable(model, 0<=x21<=4) @variable(model, 0<=x13<=12) @variable(model, 0<=x32<=9) @variable(model, 0<=x24<=14) @variable(model, 0<=x43<=7) @variable(model, 0<=x35<=20) @variable(model, 0<=x45<=4) @constraint(model, x01 + x21 == x12 + x13 ) @constraint(model, x02 + x32 + x12 == x21 + x24) @constraint(model, x13 + x43 == x32 + x35) @constraint(model, x24 == x43 + x45) @objective(model, Max, sum(x35+x45)) status = solve(model) println("x01:",getvalue(x01)) println("x02:",getvalue(x02)) println("x12:",getvalue(x12)) println("x21:",getvalue(x21)) println("x13:",getvalue(x13)) println("x32:",getvalue(x32)) println("x24:",getvalue(x24)) println("x43:",getvalue(x43)) println("x35:",getvalue(x35)) println("x45:",getvalue(x45)) println("final flow:",getvalue(x45)+getvalue(x35)) end if contains(@__FILE__, PROGRAM_FILE) @time main() end
上記のコードは下記のリポジトリでも公開しています。
上記のコードを実行すると、
下記の結果が表示されます。

上記の結果の通り、
各エッジの流量と、最終的な最大流量が計算できました。
scipyによる最大流問題の解法
続いて、同じ問題をscipy.optimize.linprogで解いてみたいと思います。
JuMPと異なり、最適化のモデリングはしてくれないので、
手計算で線形計画法の標準形に計算しなおす必要がありました。
import numpy as np from scipy.optimize import linprog c = np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, -1.0, -1.0]) A_eq = np.array([ [1.0, 0.0, -1.0, 1.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0], [0.0, 1.0, 1.0, -1.0, 0.0, 1.0, -1.0, 0.0, 0.0, 0.0], [0.0, 0.0, 0.0, 0.0, 1.0, -1.0, 0.0, 1.0, -1.0, 0.0], [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, -1.0, 0.0, -1.0], ]) b_eq = np.zeros((4,)) lb = np.zeros((10,)) ub = np.array([16.0, 13.0, 10.0, 4.0, 12.0, 9.0, 14.0, 7.0, 20.0, 4.0]) bounds = [(ilb, iub) for ilb, iub in zip(lb, ub)] result = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=bounds) print(result)
下記が実行結果です。

若干、収束判定のしきい値などにより、誤差はありますが、
ほぼJuMPと同じ結果が得られていることがわかります。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
