目次
- 目次
- はじめに
- ナップサック問題とは?
- Pythonの最適化モデリングツールcvxpyでの解法
- SciPyの混合整数計画(MILP)ソルバーで解く
- GitHubリポジトリ
- 参考資料
- MyEnigma Supporters
はじめに
以前、
Pythonの最適化モデリングツールであるcvxpyを紹介しましたが、
今回は、有名な組み合わせ最適化問題である
ナップサック問題をPythonのいくつかのツールで解いてみました。
ナップサック問題とは?
ナップサック問題は、
下記の記事のように、有名な組み合わせ最適化問題の一つです。
言葉でナップサック問題を説明すると、
ある容量(C)のナップサックに、
複数の品物を入れる際に、
その品物のサイズ(S_i)と値段(V_i)を元に、
最も値段の総和が高くなるように、
ナップサックに入れる品物を選ぶ問題です。
たまにスーパーなどでやっている、
袋詰め放題サービスで、
何をどれだけ入れれば、コスパが高いか?
という問題を考えればわかりやすいかと思います。
上記の問題を、最適化の数式で表すと、
下記のようになります。
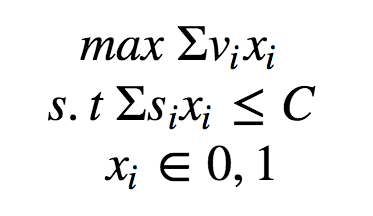
今回、その品物をナップサックに入れるかどうかが重要なので、
それぞれの品物の種類に応じたバイナリ値(0: 入れない, 1: 入れる)
を格納したベクトルを最適化における変数としました。
上記の制約を守った上で、
コスト関数を最大化するベクトルxを求めるのが目的になります。
上記の最適化式を見ると分かる通り、
ナップサック問題は線形計画問題の一つになります。
ちなみに、上記の問題のように、
変数が連続値ではなく、整数値やバイナリ値を取るような場合、
一般的なソルバーではなく、それらの問題を解くことができる
ECOS_BBのような特別なソルバーが必要になることが多いようです。
Pythonの最適化モデリングツールcvxpyでの解法
ナップサック問題は一般的に動的計画法を使って解くことが多いのですが、
今回は凸最適化の問題として、ソルバーを使って解いてみたいと思います。
今回は下記記事のナップサック問題の例題をcvxpyで解いてみました。
基本的には、前述の式をcvxpyで記述しただけです。
# # A sample code to solve a knapsack_problem with cvxpy # # Author: Atsushi Sakai (@Atsushi_twi) # import cvxpy import numpy as np size = np.array([21, 11, 15, 9, 34, 25, 41, 52]) weight = np.array([22, 12, 16, 10, 35, 26, 42, 53]) capacity = 100 x = cvxpy.Bool(size.shape[0]) objective = cvxpy.Maximize(weight * x) constraints = [capacity >= size * x] prob = cvxpy.Problem(objective, constraints) prob.solve(solver=cvxpy.ECOS_BB) result = [round(ix[0, 0]) for ix in x.value] print("status:", prob.status) print("optimal value", prob.value) print("result x:", result)
上記のコードを実行すると、
下記のようにちゃんとナップサック問題を解けていることがわかります。
(0,1,3,4,5の品物を選べば良い)

ベンチマーク
上記のコードを少し改造して、
品物の種類を10000種類まで増やしてみました。
10000種類でも、自分のMacなら5秒ほどで解くことができました。
結構早いですね。
# # A sample code to solve a knapsack_problem with cvxpy # # Author: Atsushi Sakai (@Atsushi_twi) # import cvxpy import numpy as np import random import time N_item = 10000 size = np.array([random.randint(1, 50) for i in range(N_item)]) weight = np.array([random.randint(1, 50) for i in range(N_item)]) capacity = 100 x = cvxpy.Bool(size.shape[0]) objective = cvxpy.Maximize(weight * x) constraints = [capacity >= size * x] start = time.time() prob = cvxpy.Problem(objective, constraints) prob.solve(solver=cvxpy.ECOS_BB) elapsed_time = time.time() - start print ("elapsed_time:{0}".format(elapsed_time) + "[sec]") result = [round(ix[0, 0]) for ix in x.value] print("status:", prob.status) print("optimal value", prob.value) print("result x:", result)
複数個、品物を選択出来る場合のナップサック問題の解法
前述の問題は、
与えられた品物を一個しか選べませんでしたが、
一種類の品物を複数個選べる問題も作れます。
そんな時は、Boolベクトルを正の整数のベクトルにすればOKです。
下記のようなコードで解くことできます。
# # A sample code to solve a knapsack_problem with cvxpy # # Author: Atsushi Sakai (@Atsushi_twi) # import cvxpy import numpy as np size = np.array([21, 11, 15, 9, 34, 25, 41, 52]) weight = np.array([22, 12, 16, 10, 35, 26, 42, 53]) capacity = 100 x = cvxpy.Int(size.shape[0]) objective = cvxpy.Maximize(weight * x) constraints = [capacity >= size * x] constraints += [x >= 0] prob = cvxpy.Problem(objective, constraints) prob.solve(solver=cvxpy.ECOS_BB) result = [round(ix[0, 0]) for ix in x.value] print("status:", prob.status) print("optimal value", prob.value) print("size :", size * x.value) print("result x:", result)
上記のコードを実行すると、
下記のように、4個目の商品を11個買うのがいいみたいです。
(正しいかは不明ですが..)

SciPyの混合整数計画(MILP)ソルバーで解く
SciPy1.9.0から、
混合整数線形計画ソルバーが追加されたので、こちらでも解いてみます。
https://scipy.github.io/devdocs/reference/generated/scipy.optimize.milp.html
下記がコードです。前述のcvxpyと同じ結果を得られました。
In [0]: In [12]: print("Solve Knapsack problem using scipy.optimize.milp") Solve Knapsack problem using scipy.optimize.milp In [1]: import numpy as np In [2]: from scipy.optimize import Bounds, LinearConstraint, milp In [3]: weight = np.array([22, 12, 16, 10, 35, 26, 42, 53]) In [4]: size = np.array([21, 11, 15, 9, 34, 25, 41, 52]) In [5]: capacity = 100 In [6]: integrality = np.ones_like(weight) In [7]: bounds = Bounds(0, 1) In [8]: constraints = LinearConstraint(size, ub=capacity) In [9]: res = milp(c=-weight, constraints=constraints, integrality=integrality, bounds=bounds) In [10]: res.status Out[10]: 0 In [11]: res.x Out[11]: array([1., 1., 0., 1., 1., 1., 0., 0.])
cvxpyと比べると、直接変数を0, 1に設定することができず、
整数変数であることを設定した上で、0<= x <= 1とBox制約をつけることで最適化問題的に等価にしています。
若干、cvxpyより面倒ですが、APIをシンプルにするにはしょうがないことと、
それよりもSciPyのみでナップザック問題を解けるほうが嬉しい気がしますね。
ベンチマーク
先程のCVXPYの10000個のナップザック問題のベンチマークをCVXPYでも解いてみました。
In [1]: import numpy as np In [2]: from scipy.optimize import Bounds, LinearConstraint, milp In [3]: rng = np.random.default_rng(12345) In [4]: n_item = 10000 In [5]: size = rng.integers(low=1, high=50, size=n_item) In [6]: weight = rng.integers(low=1, high=50, size=n_item) In [7]: capacity = 100 In [8]: integrality = np.ones_like(weight) In [9]: bounds = Bounds(0, 1) In [10]: constraints = LinearConstraint(size, ub=capacity) In [11]: %timeit res = milp(c=-weight, constraints=constraints, integrality=integrality, bounds=bounds) 162 ms ± 424 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
CVXPYだと5秒だったのが、SciPyでは0.16秒なので爆速ですね。。。
GitHubリポジトリ
上記のコードはすべて下記のGitHubリポジトリでも公開しています。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
