目次
- 目次
- はじめに
- Linear Time Invariant MPC: LTI-MPC
- Linear Time Varying MPC: LTV-MPC
- Nonlinear MPC
- Explicit MPC
- Hybrid MPC
- Distributed/Decentralized MPC
- Robust MPC
- Stochastic MPC
- 参考資料
- MyEnigma Supporters
はじめに
この記事は制御工学 Advent Calendar 2017 20日目の記事です。
以前、
Model Predictive Control:MPC(モデル予測制御)の概要と、
その応用例を説明しましたが、
今回は、MPCの細かい技術的分類について説明したいと思います。
Linear Time Invariant MPC: LTI-MPC
Linear Time Invariant MPC: LTI-MPCは、
最もシンプルで、広く産業界でも使用されているMPCです。
LTI-MPCでは、下記のMPCの式の通り、
システムモデルが線形で、かつ、各予測時刻において
システム行列、A, Bが常に同じであることが特徴です。
(システム行列が時刻で普遍:Time Invariant)
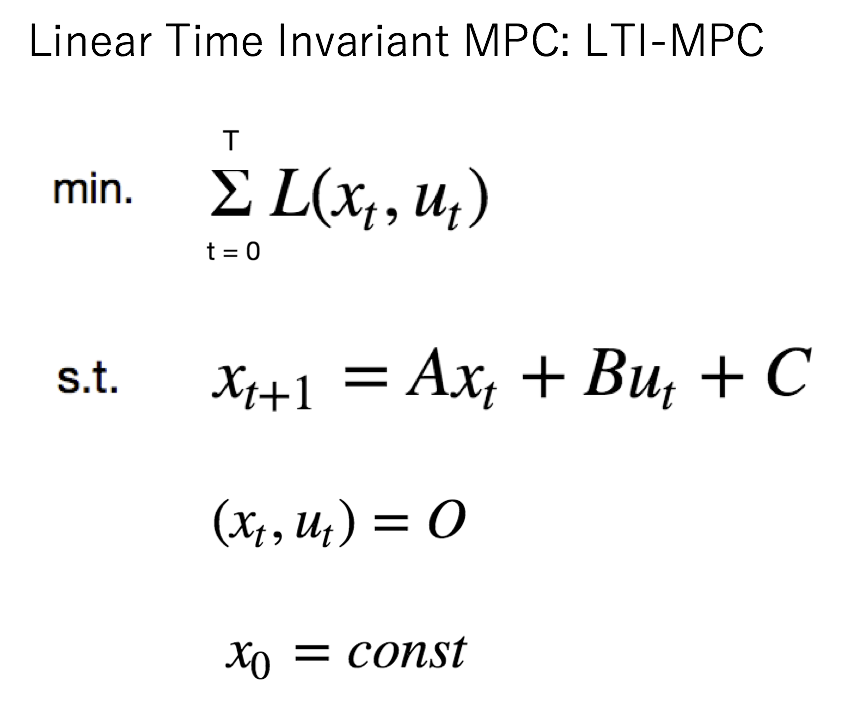
ちなみに上記の式において、Lはコストを計算する
コスト関数、Oは制約条件の集合、x0は初期状態です。
上記の式においてLとOが凸関数と凸集合である場合、
LTI-MPC問題も凸最適化問題として解くことができ、
非常に高速に計算することができます。
LTI-MPCはMPCの中では、
シンプルで高速に計算することができるので、
高周期な低レベルのコントローラに利用されたり、
後述のExplicit MPCとして実装することで、
リソースの少ない組み込み用途などにも使用されています。
Linear Time Varying MPC: LTV-MPC
Linear Time Varying MPC: LTV-MPCは
LTI-MPCと異なり、下記の式のように、
システムモデルは線形ですが、
ホライズンの各時刻において、システム行列が変化するMPCアルゴリズムです。

上記の式のように、状態と入力の制約空間Oが時刻tに応じて変化する場合も、
LTV-MPCと呼ぶことがあるようです。
LTV-MPCはLTI-MPCと同様に、
LとOtが凸関数と凸集合である場合、
凸最適化技術を使って解くことができます。
しかし、後述の通り、システム行列や制約集合が変化してしまうため、
Explicit MPCとして実装するのは難しいようです。
また、LTV-MPCはTime Varying MPCと呼ばれることもあります。
Nonlinear MPC
Nonlinear MPCは下記のような最適化式をしており、
LTI-MPCとLTV-MPCのようなLinear MPC(LMPC)と比べると、
システムモデルが非線形モデルfになっています。
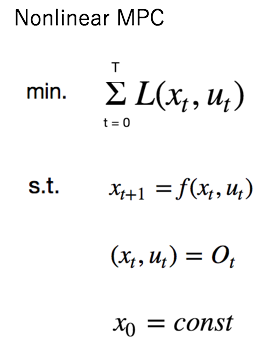
システムモデルが線形でも、
コスト関数Lや制約条件Cが凸関数、凸集合で無い場合、
それらもNonlinear MPCになります。
LMPCは凸最適化技術を使うことで高速に解を求めることができますが、
Nonlinear MPCは非線形最適化を使って解を求める必要があるため、
凸最適化に比べると、計算コストが大きくなったり、
最適解が初期値依存になってしまうという問題があります。
しかし、LMPCと比べると、
非線形モデルをそのまま扱うことが可能であり、
LMPCと比べて、良い性能が出る場合もあるようです。
Explicit MPC
Explicit MPCは、
一般的にLTI-MPCを高速に解くための手法です。
LTI-MPCは前述の通り、凸最適化を使うことで高速に解くことが可能ですが、
組み込みのコントローラなどでは、
凸最適を解くこともリソースの問題で難しい場合があります。
そのような場合、Explicit MPCでは下記の図のように、
事前に計算された線形テーブルを準備しておき、
実際に制御する場合は、
状態xからテーブルを使って線形変換することで最適入力を計算します。
事前に計算されたテーブルから線形変換の重みを検索し、
その値を使って線形変換するだけで入力を計算できるため、
非常に高速に入力を計算でき、
リソースが限られたコントローラでもMPCを実装することができます。

制御システムにもよりますが、
LTI-MPCをExplicit MPCで実装した場合、
1000倍以上計算時間が短くなる例もあるようです。
Hybrid MPC
これまで説明してきたMPCは、
入力や状態ベクトルが連続値でした。
またシステムモデルも離散時間のモデルでした。
Hybrid MPCは、
入力や状態ベクトルが連続値ではなく、
整数値だったり、Binaryの値の場合のMPCアルゴリズムです。
また、システムモデルが連続時間モデルである場合も、
Hybrid MPCが利用できます。
例えば、下記の図のように自動車システムにおいて、
アクセルとブレーキを制御して、車速を制御したい場合は
通常のMPCを使って制御できますが、
ギアシフトを含めた上で車速を制御したい場合は、
ギアシフトは連続値ではなく、整数値で設定されるため、
Hybrid MPCの技術が必要になります。

上記の例以外にも、
エンジンの制御をMPCで実施したい場合は、
エンジンの状態を離散値で表すことができるため、
Hybrid MPCが使われることがあるようです。
Hybrid MPCを解く方法としては、
Mix Integer problemを解くソルバーを利用する方法や、
各状態毎にMPC問題を分解して、
通常のMPCのロジックを使って解く方法があるようです。
詳細は下記の参考資料を参照ください。
Distributed/Decentralized MPC

Distributed/Decentralized MPCは上記のイメージ図のように、
何か非常に複雑で巨大な状態空間を持つシステムを制御したい場合に、
そのシステムを一つのMPCで制御するのではなく、
複数のMPCコントローラを協調させて制御させる手法です。
このDistributed/Decentralized MPCは、
システムの制御対象が複雑で、入力や状態量が非常に大きい時、
すべての制御を一つのコントローラで計算するのが難しい場合に、
よく使用されます。
応用例としては、
無線ネットワークの制御や、クラウドコンピュータの制御、
スマートグリッド、水路ネットワークの制御、
ビルの空調システムの制御などがあります。
下記の図はとあるヨーロッパの水路ネットワークの図であり、
かなり複雑なシステムであることがわかります。
このような場合, Distributed/Decentralized MPCが使われます。

その他にも、
ビルの空調システムをMPCで制御したい場合、
各部屋の空調はそれぞれMPCコントローラで制御しますが、
MPCコントローラの目標値や制御パラメータは、
もう一つ高次元のコントローラから制御されたり、
それぞれのMPCのコントローラが互いに情報交換することで
決定されたりします。
Robust MPC
これまで説明してきた線形MPCは、
事前に決められた線形モデルから計算された予測値が
制約条件を満たすように制御値が決定されますが、
線形モデルに誤差がある場合、
予測誤差が大きくなり、結果として実際のシステムが
制約条件を超えてしまう可能性があります。
そこで、予測値をモデルから計算される一点ではなく、
モデルの誤差を含んだ状態の集合(Reachability Set)を予測し、
その集合全体が制約を満たすように制御するアルゴリズムが
Robust MPCです。
具体的には、下記のように線形モデルにおいて、
w(t)という外乱が含まれるとして、システムをモデル化し、
そのReachability Setを計算します。
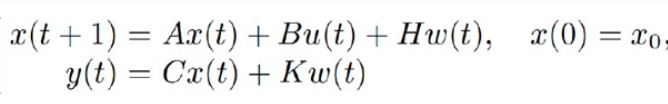
このRobust MPCは、
外乱や、モデル誤差が非常に大きい制御対象に
よく使用されるようです。
Stochastic MPC
先程のRobust MPCは、
システムモデルのモデル誤差を考慮していましたが、
これは制約の幅を確率的に推定しているだけでした。
Stochastic MPCはよりMPCに確率的な手法を取り入れたものです。
下記の図のように、状態の予測を確率モデルで記述したり、
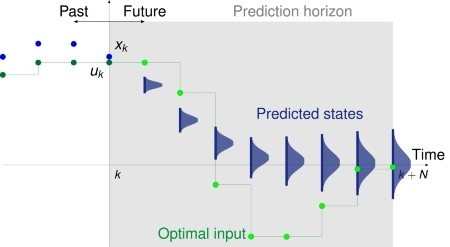
コスト関数が確率モデルの期待値で指定されることもあります。
下記の図はStochastic MPCの代表的な最適化式です。

w(t)が確率的外乱情報で、その情報を元に、
コスト関数やシステムモデル、
観測モデルの出力が計算されていることがわかります。
このStochastic MPCは、
エネルギーマネージメントシステムや、
ファイナンス分野、自動車の制御などで使用されているようです。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
