目次
- 目次
- はじめに
- Euler 法 (オイラー法)
- オイラー法における刻み距離の影響
- Runge-Kutta法(4次)
- Runge-Kutta法における刻み距離の影響
- 比較用コード(Jupyter Notebook)
- 参考資料
- MyEnigma Supporters
はじめに
ロボティクスで使われる技術では、
しばしば数値積分を実施する必要があります。
例えば、ロボットの運動モデルが下記の式のように
ある微分方程式で得られる場合、
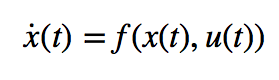
そのロボットの将来の動きを予測するために
上記の微分方程式を数値積分して予測を実現します。
この数値積分は、未来を予測するモデル予測制御や、
位置計測手法である推測航法(Dead Reckoning)などでしばしば利用されます。
上記の微分方程式の数値積分には、
いくつか代表的な手法がありますが、
今回はそれらの概要と
簡単なPythonサンプルコードによる比較結果を
を紹介したいと思います。
Euler 法 (オイラー法)
オイラー法は数値積分の手法の中で、
最もシンプルな手法です。
前述の微分方程式が与えられた時に、
各時刻tのxの値は、x(0)の初期値情報を使って、
下記のような漸化式で計算できるようになります。

オイラー法における刻み距離の影響
前述のオイラー法は非常に簡単に
積分計算を実装することができます。
よって、最も広く使われている数値積分手法であるといえます。
しかし、このオイラー法は、
刻み時間が大きいと積分の精度が悪くなるという問題があります。
下記の図は、Sin関数を各刻み距離でオイラー法を使って
積分した結果です。

dx = 0.1の時は比較的、真値に近い積分結果が得られていますが、
dx = 1.0の場合は
大きな積分誤差が発生してしまっていることがわかります。
このようにオイラー法では、
サンプリング距離が大きいと積分誤差が大きくなってしまいます。
サンプリング距離を小さくすれば、精度は向上できますが、
その分、積分回数が多くなってしまい、
計算コストが大きくなってしまうという問題があります。
Runge-Kutta法(4次)
前述の通り、オイラー法は
サンプリング幅を大きくすると精度が下がり、
サンプリング幅を小さくすると計算コストが大きくなります。
オイラー法がサンプリング幅が大きい時に
精度が悪くなってしまうのは
次のサンプリング点を計算する時に、
一つ前のサンプリング点の傾きのみから計算しているため、
サンプリング間の途中で、
傾きが変化する場合にうまく推定することができず、
積分誤差が蓄積してしまうからでです。
上記の問題を解決するために提案されたのが、
ルンゲクッタ法( Runge-Kutta法)です。
ルンゲクッタ法は、勾配を推定するサンプリング点をいくつ利用するかによって、
具体的な計算方法がかわりますが、
今回は最も広く使われている4次のルンゲクッタ法について述べます。
4次のルンゲクッタ法は4つのサンプリング点でそれぞれ勾配を計算し、
その重み付き足し算により、勾配を推定し積分を実施する手法です。
具体的には下記の式で計算されます。


4つのサンプリング点は、
区間の初め(オイラー法と同じ)と、
区間の終わり、
そして区間の中間点に二点サンプリングします。
中間点のサンプリングは、
区間の初めの勾配から計算されたサンプリング点と、
中間点の一つ目のサンプリング点の勾配から計算された
サンプリング点の二点が抽出されます。
それらを1:1:2:2で重み付き足し算し、
平均を取ったものを勾配とします。
Runge-Kutta法における刻み距離の影響
下記の図は、前述のオイラー法の比較と同様、
sin関数を使って、
Runge-Kutta法を使って数値積分を実施した結果です。

オイラー法では、刻み距離dxを大きくすると精度が低下していましたが、
Runge - Kutta法では刻み距離を大きくしても、
非常に高精度に数値積分できていることがわかります。
比較用コード(Jupyter Notebook)
下記のすべての数値積分の計算は下記のJupyter Notebookで実行されています。
参考資料
Using ode45 (Runge-Kutta 4th and 5 th order) to solve differential equations
みんな知ってるルンゲクッタ法. まだ出来ない人のためのPython実装 - Hope is a Dream. Dream is a Hope.
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。

- 作者: 齊藤宣一
- 出版社/メーカー: 共立出版
- 発売日: 2017/03/23
- メディア: 単行本
- この商品を含むブログ (1件) を見る
