目次
- 目次
- はじめに
- 凸最適化の概要と種類
- 凸最適化の専門用語
- 凸集合と凸関数
- 凸最適化の利点
- 関数の凸性の判定
- 制約付き最適化の判定法(KKT条件)
- 凸最適化の解法アルゴリズム
- 凸最適化用ツール
- 凸最適化の応用例
- より詳しく凸最適化を学びたい人は
- 参考資料
- MyEnigma Supporters
はじめに
先日、最適化技術の概要について説明しましたが、
今回は、最適化技術の一つである凸最適化(Convex Optimization)の
基礎について説明したいと思います。
凸最適化の概要と種類
凸最適化は、最適化問題の中の
ある特定の最適化問題のことを指します。
下記のような式における最適化のことを指します。
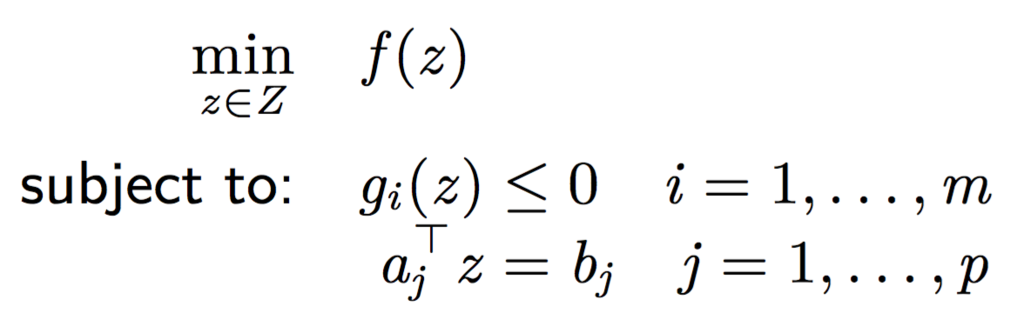
上記の式において、
コスト関数のfと不等式制約のgiはすべて凸関数である必要があります。
後述の通り、
凸最適化は、一般的な最適化問題にはない、
いくつかの利点があります。
凸最適化問題の種類としては、
下記のようなものがあります。
線形計画法 (Linear programming)
二次計画法 (Quadratic programming)
二次錐計画問題(Second-order cone programming, SOCP)
SOCPは下記のような最適化式で表されます。

SOCPでは、目的関数は線形計画法と同じですが、
不等式制約条件が、xの線形ノルムと、xの線形要素で表されるのが特徴です。
整数計画問題 (Mixed Integer programming)
下記の図のような、状態量が連続値ではなく、
不連続値(整数値)などで与えられる
整数線形計画問題も凸最適化問題の一つです。

凸最適化の専門用語
unbounded
コスト関数を小さくしようとした時に、
無限にコスト関数を小さく出来る場合のこと
infeasible
与えられた制約条件を満たす解が一つも無いこと
active, inactive
不等式条件において、
fi(x)=ciとなるxが存在している場合、
その不等式条件はactiveとなり、
存在しない場合はinactiveとなる。
redundunt
ある制約条件が、別の制約条件を含んでいる状態のこと
凸集合と凸関数
前述の最適化の式において、
その最適化の問題が、
凸最適化問題であるためには、
下記の3つ条件が必要です。
等式制約から得られる状態変数zが凸集合である
コスト関数fが凸関数である
不等式制約giが凸関数である
凸集合と凸関数の概要を下記で説明します。
Convex Set (凸集合)
Convex Setは、
下記の図のように、ある集合の任意の二点を選び、
その弦がすべて集合に含まれるような、
集合のことを指します。

一方、下記のような集合は
弦の一部が集合に含まれない二点を選ぶことができるので、
Convex Setではありません。

代表的な凸集合としては、下記があります。
アフィン空間
超平面(Hyperplanes)と、超平面で区切られた領域(halfspaces)
多面体(Polyhedra)や多胞体(Polytopes)
ベクトルノルム
楕円(Ellipsoid)
また、上記の凸集合に関して、
凸集合の交点を結んだ集合(Intersection)や、

凸集合の外部を覆った集合(Convex Hull)は、

凸集合になります。
しかし、一つ注意点として、
凸集合同士の和集合(Union)は凸集合ではなくります。

Convex function(凸関数)
入力に対して、その出力が凸集合になる関数を、
凸関数といいます。
代表的な凸関数としては、
下記のようなものがあります。
線形(アフィン) ax+b
Exponential eax
乗数 xa
絶対値の乗数 |x|^a
対数関数 log x
エントロピー -xlogx
ベクトルノルム ||x||p
行列ノルム
正の重み付き足し算
アフィン関数の足し算
凸最適化の利点
上記の凸最適化には、通常の最適化とは異なる利点があります。
1. 大域的な最適値を得ることができる。
通常の最適化問題では、
一般的に初期値から勾配情報を使って最適化を実施しますが、
この方法の場合、局所最適値にとどまってしまうことがあります。
しかし、
凸最適化の場合、目的の評価関数の凸性が担保されているため、
大域的な最適値を得ることができます。
2. 最適化の計算が早い
凸最適化の場合、内分法やアクティブセット法といった、
凸最適化特有の最適化技術を使うことにより、
汎用的な最適化手法と比べて、大規模な問題に対しても、
高速に最適化を実行することができます。
例えば、内分法の場合、
大抵の凸最適化問題は、10-50回の繰り返し計算で
解けることが知られています。
関数の凸性の判定
一般的に、ある評価関数が凸関数であるかは、
評価関数のHessianの値がすべての値に対して、半正定である必要があります。
別の言い方をすると、評価関数V(θ)に対して、
0<λ<1を満たす任意のλに対して、下記が成り立てば、
V(θ)は凸関数であるといえます。

二次計画法や線形計画法は、
制約条件が線形である場合、凸最適問題であるといえます。
制約付き最適化の判定法(KKT条件)
凸最適化のような、
制約付き最適化問題の最適化を判定する条件としては、
カルーシュ・クーン・タッカー条件(KKT条件)
がしばしば使われます。
このKKT条件は、
等式条件を入れたラグランジュの未定乗数法に、
不等式制約を入れたものだと考えることもできます。
凸最適化の解法アルゴリズム
凸最適化問題を解く方法としては、
様々なな方法が提案されていますが、
下記が代表的な方法です。
逆行列、反復無しニュートン法(制約条件が無い二次計画問題)
制約条件が無い二次計画問題の場合、
逆行列で直接最適解を計算する方法や、
反復無しのニュートン法により解くことができます。
Active set method: 有効制約法
Active set法は、比較的小規模〜中規模の
凸最適化問題を解くアルゴリズムです。
凸最適化問題の最適点が、
制約条件領域の境界上に存在することが多いという考えを利用した探索方法です。
KKT 条件に基づき、探索方向とステップサイズを繰り返し求めて最適値を計算します。
Interior point method: 内点法
Interior point法は、
大規模な凸最適化問題を解くのに利用されるアルゴリズムです。
制約条件をバリア関数を用いることで、コスト関数に組み込むことで、
制約なしの最適問題に置き換えることで、
大規模な凸最適化問題を高速に解くことを可能にします。
凸最適化用ツール
凸最適化には、
様々な環境で動作するツールがすでに提供されています。
最適化モデリングツール
凸最適化を実現したい場合、
線形計画法や二次計画法の標準形で表される問題に関しては、
後述するソルバーをそのまま利用することで凸最適化問題を解くことができます。
(それぞれの標準形に関しては上記のリンク先を参照下さい)
しかし、自分が解きたい問題が標準形とは違う形式の場合、
自分でなんとか標準形の形にできるように
最適化問題を変形する必要があるのですが、
この変換を自動的に実行してくれるのが最適化モデリングツールです。
つまり、標準形ではない形の評価関数や制約条件を記述すると、
自動的にソルバーで解けるように式変換をし、最適化を実行してくれるのです。
(もちろんどんな問題でもとけるわけではありませんが)
代表的な最適化モデリングツールは下記の通りです。
CVXPY
CVXPYはPython製の最適化モデリングツールです。
Welcome to CVXPY — CVXPY 0.4.8 documentation
オープンソースで開発されており、フリーで利用することができます。
詳しいCVXPYの使い方に関しては、下記の使用を参照下さい。
CVX
CVXはMATLAB上で動作する凸最適化モデリングツールです。
CVX: Matlab Software for Disciplined Convex Programming | CVX Research, Inc.
フリーのソルバーを使う場合はCVXも無料で利用できます。
詳しいCVXの使い方に関しては、下記を参照下さい。
YALMIP
YALMIPもMATLAB上で動作するフリーの最適化モデリングツールです。
先程のCVXは凸最適化のみ利用できますが、
YALMIPの場合はその他の汎用的な最適化問題にも利用可能です。
AMPL
AMPLは商用の最適化モデリングツールです。
非常に広い範囲の最適化問題や、ソルバーに対応しています。
cvxgen
cvxgenは、あるモデリング言語で記述した
凸最適化問題を高速に解くことができる
C言語のコードを生成できるWebツールです。
JuMP
プログラミング言語Julia製のフリーの最適化モデリングツールです。
Juliaが高速な計算が可能な言語なので、
JuMPを使うと高速に最適化計算をすることができます。
また、非線形最適化にも対応しているのも便利です。
詳細は下記を参照ください。
GAMS
GAMSも商用の最適化モデリングツールです。
非常に多くのソルバーや、最適化問題に対応しています。
Pyomo
PyomoはPython製のオープンソースの最適化モデリングツールです。
凸最適化だけでなく、非線形最適化問題も解くことができます。
PC向け凸最適化ソルバー
下記は凸最適化ソルバーです。
自分の解きたい問題が、
線形計画法や二次計画法の標準形で簡単に表すことが出来る場合は、
下記のソルバーを単体で使うと便利です。
ちなみに、前述のモデリングツールも、
下記のソルバーを内部で使っています。
cvxopt
cvxoptはPython製のフリーの凸最適化ソルバーです。
cvxoptの詳しい使い方は下記を参照下さい。
Ipopt
IpoptはC++で書かれた大規模システム用の最適化ソルバーです。
基本的には非線形最適化のソルバーですが、
凸最適化も高速に解くことができることがあります。
IpoptはC++だけでなく、MATLABやJava, R, Fortran, Python, C#などの
インターフェイスが準備されており、それらの言語からも利用可能です。
SeDuMi
SeDuMiはMATLABやOctaveから利用可能なフリーなソルバーです。
SDPT3
SDPT3もMATLAB上で利用可能なフリーのソルバーです。
GPLライセンスで公開されています。
IBM CPLEX
CPLEXはIBMが開発、販売している商用ソルバーです。
オペレーションズ・リサーチなどの分野ではかなり広く利用されているようです。
Gurobi
Gurobiも商用ソルバーの一つです。
前述のAMPLとの連携や、Pythonインターフェイスの充実などの特徴があります。
MOSEK
MOSELも商用ソルバーの一つです。
二次凸問題を非常に高速に解くことができる特徴ががあります。
組み込み用凸最適化ソルバー
前述のソルバーは、ほとんどPC上で動くことを仮定しており、
組み込みシステムや、高速で最適化問題を解きたい場合には、
あまり適していません。
そこで下記は、組み込みに利用できるソルバーや、
組み込み用のコードを自動生成できるツールになります。
qpOASES
qpOASESはフリーのC++ソルバーです。
モデル予測制御のような用途において、
高速に計算可能な最適化を実現することができます。
ライセンスはLGPLです。
OOQP
OOQPは二次計画法を解くための
オブジェクト指向で書かれたC++ライブラリです。
ECOS
ECOSはCで書かれたオープンソースのソルバーです。
PythonやMATLABのインターフェイスも準備されています。
CVXGEN
CVXGENは比較的小規模の二次形式問題を解くための、
Cコードを自動生成することができるモデリングツールです。
CVXGEN: Code Generation for Convex Optimization
最適化問題を非常に高速に解くことが可能になります。
FiOrdOs
FiOrdOsは、二次計画法を解くためのCコードを生成することができる
MATLABライブラリです。
FORCES or (FORCES PRO)
FORCESは内分法による最適化のコードを生成することができるMATLABライブラリです。
モデル予測制御などにおいて、高速に問題を解くことができるコードを生成してくれます。
FORCES PROという商用ライセンスも販売しています。
凸最適化の応用例
線形計画法の応用例
下記の記事を参照ください。
ポートフォリオ最適化
金融工学の有名な問題の一つである
ポートフォリオ最適化問題も凸最適化問題の一つです。
ポートフォリオ最適化問題は、
複数の投資先(アセット)に、
それぞれどれだけ投資すれば良いかという最適化問題です。
画像復元
下記のプレゼン資料にある通り、
ある画像の一部が欠けている時に、
凸最適化を使って隣接ピクセルの分散を最小化するようにすると、
欠けている画像部分を復元することができます。
H2O World - Consensus Optimization and Machine Learning - Stephen Boyd
例えば、下記のように一部の写真が文字で欠けている画像でも、

下記のように、非常に美しく画像が復元できたり、

下記のように80%の画像データが失われてる状態でも、

下記のように復元できます。

サポートベクターマシン
機械学習の技術で有名なサポートベクターマシンは、
凸最適化を使って、分類を実施します。
詳細は下記の記事を参照ください。
線形MPC(モデル予測制御)
制御技術の一つである線形MPC(モデル予測制御)は
リアルタイムに凸最適化を解くことで、
制御を実施するアルゴリズムです。
詳細は下記を参照ください。
より詳しく凸最適化を学びたい人は
こちらの資料がおすすめです。
![Convex Optimization【電子書籍】[ Stephen Boyd ] Convex Optimization【電子書籍】[ Stephen Boyd ]](https://thumbnail.image.rakuten.co.jp/@0_mall/rakutenkobo-ebooks/cabinet/0780/2000002730780.jpg?_ex=128x128)
Convex Optimization【電子書籍】[ Stephen Boyd ]
- ジャンル: 本・雑誌・コミック > 洋書 > BUSINESS & SELF-CULTURE
- ショップ: 楽天Kobo電子書籍ストア
- 価格: 7,843円
英語の書籍ですが、
世界的に凸最適化のデファクトスタンダードの教科書として扱われています。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
