目次
- 目次
- はじめに
- 制約付き非線形最小二乗法
- 制約付き非線形最小二乗法の解法1: ペナルティ法
- 制約付き非線形最小二乗法の解法2: 拡張ラグランジュ法
- 制約付き非線形最小二乗法の応用例1: 自動車の非線形制御
- 制約付き非線形最小二乗法の応用例2: 後処理軌跡推定
- 参考資料
- MyEnigma Supporters
はじめに
スタンフォード大学には
機械学習を学ぶ上での第一歩として、
Introduction to Matrix Methods (EE103)という授業があります。
今回の記事では、
この授業の教科書である
Introduction to Applied Linear Algebraを
読んだ際の技術メモです。
この教科書は下記のリンクのページから
pdfをダウンロードすることができます。
本記事では、
上記の教科書の非線形最小二乗法の部分のみのメモです。
他の部分に関しては、下記の記事を参照下さい。
制約付き非線形最小二乗法
制約付き非線形最小二乗法は、
非線形関数f(x)とg(x)において、
下記のような最適化問題を解く方法を指します。
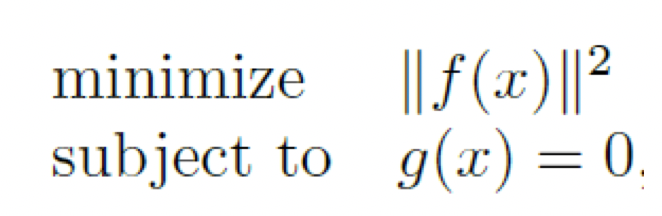
制約条件g(x) = 0 が線形の場合は、
下記の記事で述べたレーベンバーグ・マーカート法のStep2で
線形方程式を毎回解くことで、最適化問題を解くことができます。
しかし、g(x)=0が非線形の場合、
最適化問題を解くのは、より一層難しくなります。
このような制約付き非線形最小二乗法を解く方法としては、
代表的なものとして、ペナルティ法と拡張ラグランジュ法があります。
制約付き非線形最小二乗法の解法1: ペナルティ法
ペナルティ法は、制約条件g(x) = 0を満たすように、
g(x)をコスト関数にいれた下記のようなコスト関数を最小化する方法です。
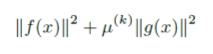
上記のコスト関数を最小化すると、自ずとg(x)も0に近づき、
g(x)=0の制約条件を満たすようになることがわかります。
またペナルティ法では、g(x)のコスト関数の重みであるλを、
反復のたびに、大きくしていくことで収束性を高める方法が取られます。
制約付き非線形最小二乗法の解法2: 拡張ラグランジュ法
前述のペナルティ法は、制約付き非線形最小二乗法を解くことができますが、
実際にg(x) = 0とするためには、
μを非常に大きくする必要があり、
それをコンピュータで実現するのは難しく、
またμの増加の方法によっては、うまく収束しない場合があります。
このような問題を解決する方法が拡張ラグランジュ法です。
1960年台に開発されました。
拡張ラグランジュ法は、
前述のペナルティ法と、
以前紹介したラグランジュの未定乗数法を組み合わせたアルゴリズムです。
ペナルティ法と比べると、あまりμを大きくしなくても、
g(x) = 0を満たすような形になり、
収束性が高いという特徴があります。
拡張ラグランジュ法では、
3つのステップを繰り返し計算することで、
制約付き非線形最小二乗法を解きます。
- Step1:下記の非線形最小二乗法をレーベンバーグ・マーカートなどで解く
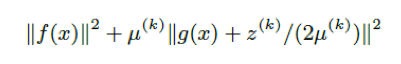
ここで、μはペナルティ項の重みであり、zはラグランジュ定数です。
それぞれ、μ=1, z = 0で初期化しておきます。
- Step2: zを更新する
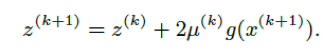
これにより、ラグランジュの未定乗数法の収束条件に近づきます。
- Step3: μを更新する
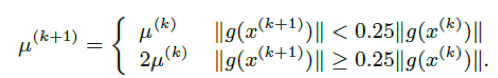
これによりペナルティ項が収束条件に近づきます。
制約付き非線形最小二乗法の応用例1: 自動車の非線形制御
この記事では、この教科書の429Pで説明されている
自動車の非線形制御の簡単なシミュレーションを、
Juliaと最適化モデリングツールであるJuMPを使って解いてみます。
詳細は教科書を見ていただきたいのですが、
基本的には、x, y, yawの二次元の車両の最終位置を指定すると、
シンプルな車両モデルを元に、その最終位置までの
速度とステアリング角度の予測値を制約付き非線形最小二乗法で計算してくれます。
下記がJuliaのコードです。
# # Nonlinear vehicle control # # author: Atsushi Sakai # # see: Boyd, Stephen, and Lieven Vandenberghe. # Introduction to Applied Linear Algebra: Vectors, Matrices, and Least Squares. # Cambridge University Press, 2018. P429 # using JuMP using Ipopt using PyPlot function solve_nonlinear_vehicle_control(xfinal, N, gamma, L, dt) solver=IpoptSolver(print_level=0) model = Model(solver=solver) nx = 3 nu = 2 @variable(model, x[k=1:nx,t=1:N]) @variable(model, u[k=1:nu,t=1:N]) # initial and terminal constraint @constraint(model, x[:,1] .== [0.0; 0.0; 0.0]) @constraint(model, x[:,N] .== xfinal) initx = zeros(nx, N) for k in 1:N-1 # vehicle model @NLconstraint(model, x[1,k+1] == x[1,k] + dt*u[1,k]*cos(x[3,k])) @NLconstraint(model, x[2,k+1] == x[2,k] + dt*u[1,k]*sin(x[3,k])) @NLconstraint(model, x[3,k+1] == x[3,k] + dt*u[1,k]/L*tan(u[2,k])) initx[:,k] = xfinal*k/N end initx[:,N] = xfinal setvalue(x,initx)# warm starting # object function obj = sum(sum(u[:, i].^2 for i=1:N)) obj += gamma*sum(sum((u[:, i+1]-u[:, i]).^2 for i=1:N-1)) @objective(model, Min, obj) status = solve(model) println(status) x_opt = getvalue(x) u_opt = getvalue(u) display(x_opt) # display(u_opt) return x_opt, u_opt end function main() println(PROGRAM_FILE," start!!") xfinal = [-1.0;1.0;deg2rad(90)] N = 50 # control steps gamma = 10.0 #weight for diff of input L = 0.1 # Wheel base dt = 0.1 # time tick x, u = solve_nonlinear_vehicle_control(xfinal, N, gamma, L, dt) plot(x[1,:], x[2,:], "-r") plot(xfinal[1], xfinal[2], "ob") axis("equal") show() println(PROGRAM_FILE," Done!!") end
下記のGitHubリポジトリでも公開しています。
上記のコードを実行すると、
下記のように、指定したx,y,θへの非線形の軌跡を
制約付き最小二乗法によって計算してくれます。

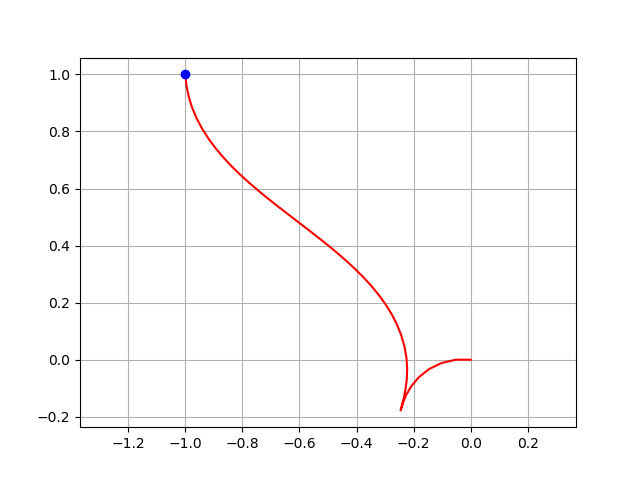
制約付き非線形最小二乗法の応用例2: 後処理軌跡推定
続いて、ロボットにおける後処理軌跡推定を
制約付き最小二乗法で解いてみたいと思います。
後処理軌跡推定の詳細に関しては、下記を参照ください。
前回は、C++の最適化ライブラリであるCeres Solverを使いましたが、
今回はJuliaのJuMPを使いたいと思います。
下記がJuliaのコードです。
# # Trajectory Estimzation with nonlinear optimization # # Assume the robot can get dead-reckoning and GPS positioning data. # # author: Atsushi Sakai # using JuMP using Ipopt using PyPlot function optimize_trajectory(h_x, h_z, h_u, dt, lamda) solver=IpoptSolver(print_level=0) model = Model(solver=solver) N = size(h_x)[2] nx = 3 nu = 2 @variable(model, x[k=1:nx,t=1:N]) @variable(model, u[k=1:nu,t=1:N]) # initial constraint @constraint(model, x[:,1] .== [0.0; 0.0; 0.0]) for k in 1:N-1 # vehicle model @NLconstraint(model, x[1,k+1] == x[1,k] + dt*u[1,k]*cos(x[3,k])) @NLconstraint(model, x[2,k+1] == x[2,k] + dt*u[1,k]*sin(x[3,k])) @NLconstraint(model, x[3,k+1] == x[3,k] + dt*u[2,k]) end setvalue(x, h_x)# warm starting setvalue(u, h_u)# warm starting @NLobjective(model, Min, sum( (x[1,k+1] - (x[1,k] + dt*h_u[1,k]*cos(x[3,k])))^2 + (x[2,k+1] - (x[2,k] + dt*h_u[1,k]*sin(x[3,k])))^2 + (x[3,k+1] - (x[3,k] + dt*h_u[2,k]))^2 for k in 1:N-1) +lamda*sum( (x[1,k] - h_z[1,k])^2 + (x[2,k] - h_z[2,k])^2 for k in 1:N-1 if h_z[1,k] != 0.0 )) status = solve(model) println(status) x_opt = getvalue(x) u_opt = getvalue(u) display(x_opt) return x_opt, u_opt end function predict_motion(x, u, dt) x[1]=x[1]+u[1]*dt*cos(x[3]) x[2]=x[2]+u[1]*dt*sin(x[3]) x[3]=x[3]+u[2]*dt return x end function add_input_noize(u,Q) un=u[:] un[1]=un[1]+randn()*Q[1] un[2]=un[2]+randn()*Q[2] return un end function gps_observation(xTrue, time, zdt, R) z=[0.0, 0.0] if abs(time%zdt) > 0.01 return z end z[1]=xTrue[1]+randn()*R[1] z[2]=xTrue[2]+randn()*R[1] return z end function simulate(u, SIMTIME, DT, ZDT, Q, R) h_xTrue = zeros(3,0) h_x = zeros(3,0) h_z = zeros(2,0) h_u = zeros(2,0) xTrue = [0.0, 0.0, 0.0] x = [0.0, 0.0, 0.0] for time=0.0:DT:SIMTIME xTrue = predict_motion(xTrue, u, DT) ud = add_input_noize(u, Q) x = predict_motion(x, ud, DT) z = gps_observation(xTrue, time, ZDT, R) # save history h_xTrue = hcat(h_xTrue, xTrue) h_x = hcat(h_x, x) h_z = hcat(h_z, z) h_u = hcat(h_u, u) end return h_xTrue, h_x, h_z, h_u end function main() println(PROGRAM_FILE," start!!") SIMTIME = 50.0 DT = 0.1 # time tick for control ZDT = 4.0 # time tick to get observation Q = [0.5,0.1] #input noise u = [1.0,0.1]# input v[m/s],omega[rad/s] R=[0.1] #observation noise h_xTrue, h_x, h_z, h_u = simulate(u, SIMTIME, DT, ZDT, Q, R) lamda = 0.1 # weight for observation residual x_opt, u_opt = optimize_trajectory(h_x, h_z, h_u, DT, lamda) close() plot(h_xTrue[1,:], h_xTrue[2,:], ".b", label="Ground Truth") plot(h_x[1,:], h_x[2,:], ".g", label="Dead Recknoing") plot(h_z[1,:], h_z[2,:], "xg", label="GPS Observation") plot(x_opt[1,:], x_opt[2,:], "-r", label="Optimized trajectory") legend() axis("equal") println(PROGRAM_FILE," Done!!") end @time main()
下記のGitHubリポジトリでも公開しています。
上記のJuliaコードを実行すると、
下記のような結果が得られます。

青線が真のロボットの軌跡、
緑線がオドメトリの軌跡(ノイズにより精度が低下)
緑バツがGPSの位置(精度は良いですが、データの取得間隔が長い)
そして、赤線が最適化後の軌跡です。
この赤線の結果を見ると分かる通り、
オドメトリとGPSのデータを使って、
軌跡全体が真の軌跡に近づき、
高精度に推定出来ていることがわかります。
(カルマンフィルタなどを使った場合は、
GPSが取得された点以外は補正されません)
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
