Pythonによる数理最適化入門 (実践Pythonライブラリー)

posted with カエレバ

並木誠朝倉書店 2018-04-09

Amazonで探す

楽天市場で探す

Yahooショッピングで探す

目次
はじめに
線形計画法の概要
線形計画法を解く方法
- シンプレックス(単体法)
- 内点法
Pythonによる線形計画法の解き方
- cvxoptを使う方法
- scipyを使う方法
Juliaにおける線形計画法の解き方
最大流問題(Max Flow Problem)の解き方
最小コストネットワークフロー問題
より詳しく線形計画法を学びたい人は
参考資料
MyEnigma Supporters

はじめに

先日、最適化問題の一つの方式として二次計画法の概要と、

Pythonでの解き方を紹介しましたが、

myenigma.hatenablog.com

今回はもっと多くの分野で使われている

最適化問題の一つである

線形計画法(Linear Programming)の概要と、

同じくいくつかの言語やライブラリでの

解き方を紹介したいと思います。

線形計画法の概要

線形計画法は、

下記の式のように、

変数が複数の一次不等式や等式によって制約が与えられている時に、

ある一次のコスト関数を最大・最小化させる方法です。

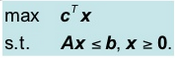
制約条件の不等式は、

非負の変数であるスラック変数という変数を導入することで、

等式制約に変換することができます。

myenigma.hatenablog.com

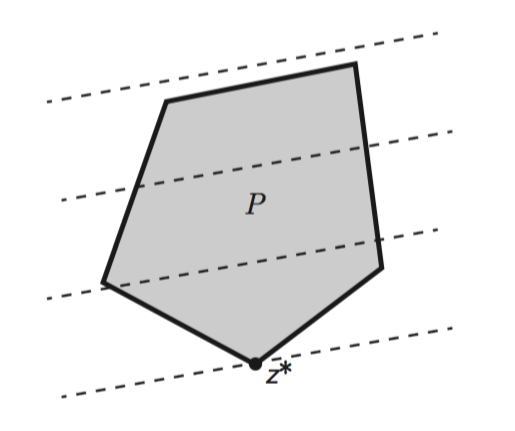
線形計画法を二次元の図に表すと下記のようになります。

Pは制約条件による、状態ベクトルzが取りうる範囲を表しており、

点線はコスト関数の等高線を表しています。

線形計画法の場合、コスト関数の等高線は直線で表されます。

この線形計画法は、非常に多くの学問において利用されており、

工学だけでなく、経済学や経営学でも広く利用されています。

特にオペレーションズ・リサーチ（OR）と呼ばれる、

様々な計画に対して最も効率的に行う方法を求める学問では、

この線形計画法が非常に広く使われています。

また、各パラメータを少し変更した時に、

最適値がどのように変化するのかを分析する

感度分析(Sensitibity Analayis)など、

様々な実用化のための技術も開発されている分野です。

線形計画法を解く方法

これまで様々な線形計画問題を解く

アルゴリズムが提案されてきましたが、

以下の２つのアルゴリズムが特に有名です。

シンプレックス(単体法)

この線形計画法を解く上で重要な考え方として、

それぞれの制約条件によって決定する

変数の可能領域を表す多次元凸多面体の頂点にのみ

最適解がある

ということです。

これは、コスト関数や制約上限が一次関数なので、

極値を多面体内部や辺上で取らないためです。

　この考え方を元にした、線形計画問題の解法アルゴリズムが

シンプレックス法です。

シンプレックス法 - Wikipedia

このアルゴリズムは、上記の考え方利用して、

変数の可能領域のある頂点から、コスト関数が改善する方向に、

頂点を移動しながら、最適値を求めるアルゴリズムになります。

単純に大規模な線形計画問題を解く場合は、

後述の内点法の方が、解を求めるまでの計算コストが少ないと言われていますが、

シンプレックス法は、一度解いた線形計画問題に、制約などを追加したときに、

前回の計算結果を初期解として、高速に再計算できるなどの特徴があるため、

発明されたのは、1950年ぐらいとかなり古いですが、

未だに線形計画問題の解法として利用されるアルゴリズムです。

また、このシンプレックス法は、

状態変数の数よりも、制約条件の数に計算時間が影響しやすいため、

制約条件の数が多い場合は、主問題を解くよりも、

双対問題を解くテクニックもあります。

双対問題に関しては、下記を参照ください

myenigma.hatenablog.com

内点法

もう一つの有名なアルゴリズムが、内点法です。

特に双対問題を交互に解く、

主双対内点法(Primal-dual interior-point method)が有名です。

ja.wikipedia.org

qiita.com

Pythonによる線形計画法の解き方

では、実際にPythonを使って、

線形計画法を解いてみたいと思います。

cvxoptを使う方法

線形計画法のソルバーとしては、

先日、二次計画法の際に紹介したPython最適化ソルバー

cvxoptに線形計画法を解く機能があるので、

こちらを利用したいと思います。

myenigma.hatenablog.com

解く問題としては、

下記の書籍のP171の例題を

実際にPythonを使って解いてみたいと思います。

これなら分かる最適化数学: 基礎原理から計算手法まで

作者:健一, 金谷
共立出版

Amazon

まずx1,x2,x3,x4の４つの変数があり、

等式制約は下記の通りとします。

また、各変数はすべて０以上という不等式制約もあるとします。

最後に最終的な目的は下記の評価関数を最大化したいと思います。

cvxoptでは、

線形計画法を解く場合はsolvers.lpというメソッドを使います。

Cone Programming — CVXOPT User's Guide

lpはコスト関数の最小値を求める関数なので、

今回のような最大値を求める問題の場合は

コスト関数の各変数の符号を逆転することで、

最大値を求めることができます。

(下記のコードでは、行列cの部分がマイナスになっている)

また不等式制約についても、

lpの前提条件と問題の条件が逆なので、

係数がマイナスになっていることに注意が必要です。

下記のコードでは、Gとhが不等号制約、

Aとbが等号制約を表しています。

"""
Simple sample code to solve linear programming with cvxopt

author Atsushi Sakai
"""

import numpy

import cvxopt
from cvxopt import matrix

c = matrix(numpy.array([-29.0, -45.0, 0.0, 0.0]))
G = matrix(numpy.diag([-1.0, -1.0, -1.0, -1.0]))
h = matrix(numpy.array([0.0, 0.0, 0.0, 0.0]))
A = matrix(numpy.array([[2.0, 8.0, 1.0, 0.0], [4.0, 4.0, 0.0, 1.0]]))
b = matrix(numpy.array([60.0, 60.0]))

print("c:")
print(c)
print("G:")
print(G)
print("h:")
print(h)
print("A:")
print(A)
print("b:")
print(b)

sol = cvxopt.solvers.lp(c, G, h, A, b)

print("x:", sol["x"])
print("obj:", sol["primal objective"])

下記が実際に上記のコードを実行した結果になります。

先程の書籍にある通り、

解の答えはx1=10,x2=5,x3=0,x4=0で最大値f=515なので、

fの符号を反転していることを考えると、

ちゃんと正しい値が計算できていることがわかります。

上記のコードは下記でも公開しています。

github.com

scipyを使う方法

Pythonの科学技術ライブラリとして有名なscipyにも、

内点法による線形計画法を解く関数であるlinprogがあります。

docs.scipy.org

下記はこのlinprogを使って、先程のcvxoptで解いた問題と

同じ問題を解くサンプルコードです。

from scipy.optimize import linprog
import numpy as np

c = np.array([-29.0, -45.0, 0.0, 0.0])
A_ub = np.diag([-1.0, -1.0, -1.0, -1.0])
b_ub = np.array([0.0, 0.0, 0.0, 0.0])
A_eq = np.array([[2.0, 8.0, 1.0, 0.0], [4.0, 4.0, 0.0, 1.0]])
b_eq = np.array([60.0, 60.0])

result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq)
print(result)

下記が実行結果です。

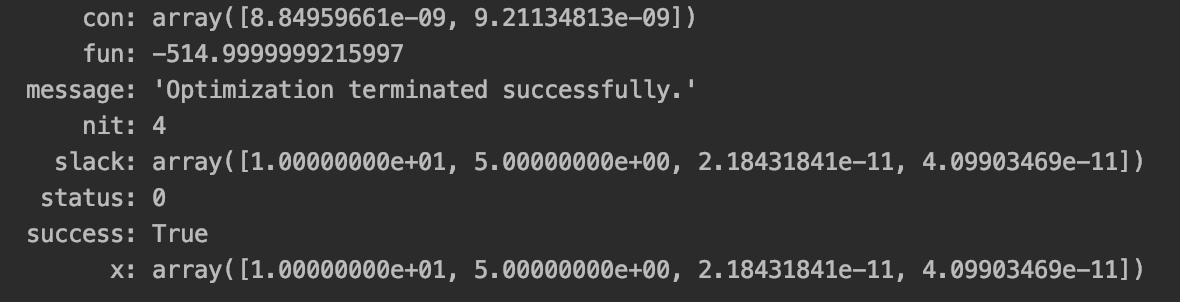
先程のcvxoptと同じ結果が得られていることがわかります。

個人的には、scipyは様々なPython環境ですでにインストールされていることが多く、

またnumpyのarrayを直接入力できるので、

cvxoptより、より手軽に線形計画法を解くことができると思います。

Juliaにおける線形計画法の解き方

続いて、Juliaという比較的新しいプログラム言語で

線形計画法を解いてみたいと思います。

myenigma.hatenablog.com

今回はJuMPというJuliaの最適化ライブラリを使うことにします。

myenigma.hatenablog.com

シンプルな線形計画問題

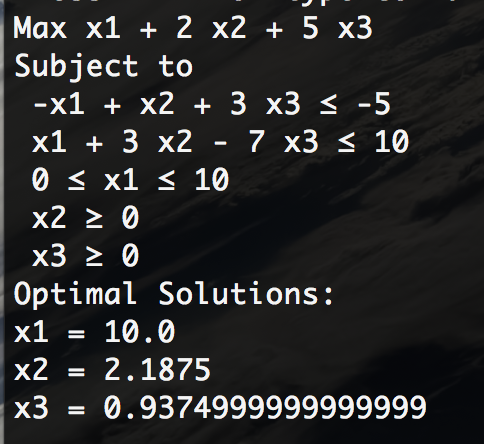
下記のシンプルな線形計画問題を解いてみたいと思います。

上記の問題を解く、Juliaのコードは下記の通りです。

using JuMP
using Clp

m = Model(solver=ClpSolver())

@variable(m, 0<= x1 <=10)
@variable(m, x2 >=0)
@variable(m, x3 >=0)

@objective(m, Max, x1 + 2*x2 + 5*x3)

@constraint(m, -x1 +  x2 + 3*x3 <= -5)
@constraint(m,  x1 + 3*x2 - 7*x3 <= 10)

print(m)
status = solve(m)

println("Optimal Solutions:")
println("x1 = ", getvalue(x1))
println("x2 = ", getvalue(x2))
println("x3 = ", getvalue(x3))

https://github.com/AtsushiSakai/JuliaSamples/blob/master/JuMP/convex_opt/LP1.jlgithub.com

上記を実行すると、下記のように線形計画問題を解くことができます。

シンプルな線形計画問題2

以前、cvxpyで解いたシンプルな線形計画問題をJumpで解いてみました。

myenigma.hatenablog.com

using JuMP
using Mosek

function main()
    println("JuMP sample2")
    model = Model(solver=MosekSolver())

    @variable(model, 2.5 <= z1 <= 5.0)
    @variable(model, -1.0 <= z2 <= 1.0)
    @NLobjective(model, Min, abs(z1+5.0) + abs(z2-3.0))

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("z1:",getvalue(z1))
    println("z2:",getvalue(z2))
end

main()

https://github.com/AtsushiSakai/JuliaSamples/blob/master/JuMP/convex_opt/sample2.jlgithub.com

上記を実行すると下記のように、

cvxpyで同じ問題を解いた時と同じ結果が得られます。

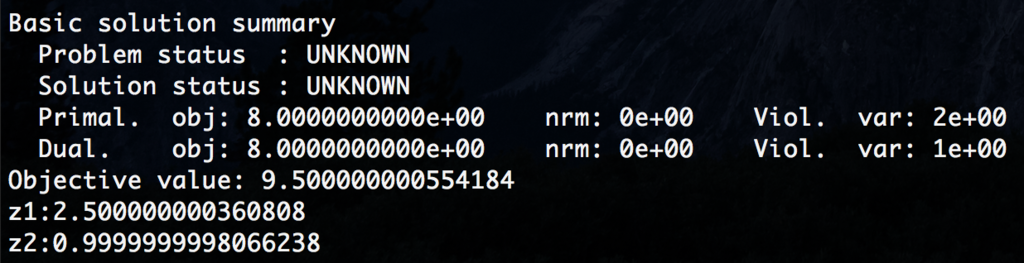
一つ注意点として、abs関数をコスト関数の中で利用する場合は、

@objectiveではなく、@NLobjectiveを使う必要があるみたいです。

stackoverflow.com

下記はその他のサンプルです。

using JuMP
using Ipopt

function main()
    println("JuMP sample3")
    model = Model(with_optimizer(Ipopt.Optimizer))

    @variable(model, z1>=0.0)
    @variable(model, z2>=0.0)
    @objective(model, Min, 3.0*z1 + 2.0*z2)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = optimize!(model)
    println("Objective value: ", objective_value(model)) 
    println("z1:",value(z1))
    println("z2:",value(z2))
end

main()

function main3()
    println("JuMP sample5")
    model = Model(solver=MosekSolver())

    @variable(model, z1>=0.0)
    @variable(model, z2>=0.0)
    @objective(model, Min, z1-z2)
    @constraint(model, z1-z2>=30)
    @constraint(model, 2.0*z1+z2>=1)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("z1:",getvalue(z1))
    println("z2:",getvalue(z2))
end

main3()

function main5()
    println("JuMP sample7")
    model = Model(solver=MosekSolver())

    @variable(model, z1>=1.0)
    @variable(model, z2>=1.0)
    @objective(model, Min, z1^2+z2^2)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("z1:",getvalue(z1))
    println("z2:",getvalue(z2))
end

function main8()
    println("JuMP sample8")
    model = Model(solver=MosekSolver())

    @variable(model, z1>=0.0)
    @variable(model, z2>=0.0)
    @variable(model, z3>=0.0)
    @objective(model, Min, 0.5*(z1^2+z2^2+0.1*z3^2)+0.55*z3)
    @constraint(model, z1+z2+z3==1)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("z1:",getvalue(z1))
    println("z2:",getvalue(z2))
    println("z3:",getvalue(z3))
end

JuMPによる最小二乗法解法サンプルコード

以前、cvxpyで解いた最小二乗法問題をJumpで解いてみました。

myenigma.hatenablog.com

using JuMP
using Mosek

function main()
    println("JuMP sample1")
    model = Model(solver=MosekSolver())
    m = 10
    n = 5
    A = rand(m, n)
    b = rand(m, 1)
    println(A)
    println(b)

    @variable(model, 0.0<=x[1:size(A,2)]<=1.0)
    @objective(model, Min, sum((A*x-b).^2))

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("x:",getvalue(x))
end

main()

https://github.com/AtsushiSakai/JuliaSamples/blob/master/JuMP/convex_opt/sample1.jlgithub.com

すると下記のように最小二乗法の計算結果が得られます。

modelをprintすると、

最適化問題が数式みたいに表示されるのはいい感じですね。

ただ行列をprintした時に、

行と列で綺麗に表示されないのが悲しい。。。

JuMPによる混合整数最適化問題の解法

続いて、

下記の２つの混合整数(Mixed integer)最適化問題をJuMPを使って解いてみます。

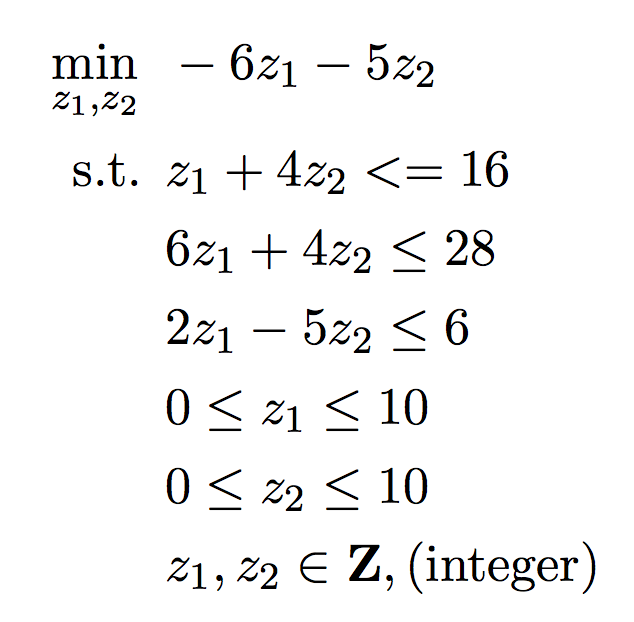
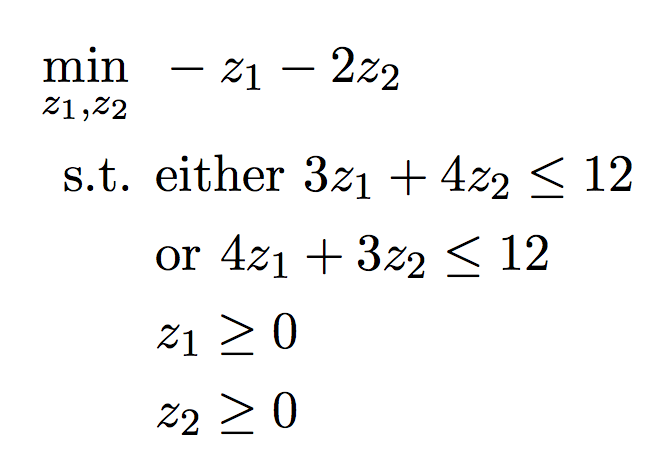
下記がJuliaのサンプルコードです。

今回はMixed integerを解くことができる。

MosekとCPLEXをソルバーとして使っています。

using JuMP
using Mosek
using CPLEX

function main1()
    println("JuMP mix integer sample1")
    model = Model(solver=MosekSolver())

    @variable(model, z1, Int)
    @variable(model, z2, Int)
    @objective(model, Min, -6*z1-5*z2)
    @constraint(model, z1+4*z2<=16)
    @constraint(model, 6*z1+4*z2<=28)
    @constraint(model, 2*z1-5*z2<=6)
    @constraint(model, 0<=z1<=10)
    @constraint(model, 0<=z2<=10)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("z1:",getvalue(z1))
    println("z2:",getvalue(z2))
end

function main2()
    println("JuMP mix integer sample2")
    model = Model(solver=CplexSolver())

    @variable(model, z1>=0)
    @variable(model, z2>=0)
    @variable(model, z3, Bin)
    @objective(model, Min, -z1-2*z2)
    @constraint(model, 3*z1+4*z2-12<=4*z3)
    @constraint(model, 4*z1+3*z2-12<=4*(1-z3))

    println("The optimization problem to be solved is:")
    println(model)

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("z1:",getvalue(z1))
    println("z2:",getvalue(z2))
    println("z3:",getvalue(z3))
end

main1()
main2()

https://github.com/AtsushiSakai/JuliaSamples/blob/master/JuMP/mix_integer_opt/sample.jlgithub.com

JuMPによるナップサック問題の解法サンプルコード

以前cvxpyで解いたナップサック問題を

JuMPで解いてみました。

myenigma.hatenablog.com

using JuMP
using Mosek

function main()
    println("JuMP knapsack")
    model = Model(solver=MosekSolver())

    size = [21, 11, 15, 9, 34, 25, 41, 52]
    weight = [22, 12, 16, 10, 35, 26, 42, 53]
    capacity = 100

    @variable(model, x[1:length(size)], Bin)
    @objective(model, Max, dot(weight,x))
    @constraint(model, dot(size, x) <= capacity)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("Solution is:")
    for i = 1:length(size)
        println("x[$i] = ", getvalue(x[i]))
    end
end

main()

https://github.com/AtsushiSakai/JuliaSamples/blob/master/JuMP/convex_opt/knapsack.jlgithub.com

下記のようにちゃんとcvxpyの時と同じ結果が得られています。

注意点としては、最適化変数をboolenにしたい時は、

Boolを与えるのではなく、JuMP専用のbinを型として与える必要があります。

続いて、同じくcvxpyでも実施した

一つの商品を複数回選んで良い場合のコードはこちらです。

using JuMP
using CPLEX

function main()
    println("JuMP knapsack")
    model = Model(solver=CplexSolver())

    size = [21, 11, 15, 9, 34, 25, 41, 52]
    weight = [22, 12, 16, 10, 35, 26, 42, 53]
    capacity = 100

    @variable(model, x[1:length(size)], Int)
    @constraint(model, x .>= 0)
    @objective(model, Max, dot(weight,x))
    @constraint(model, dot(size, x) <= capacity)

    println("The optimization problem to be solved is:")
    println(model) # Shows the model constructed in a human-readable form

    status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
    println("Solution is:")
    for i = 1:length(size)
        println("x[$i] = ", getvalue(x[i]))
    end
end

main()

https://github.com/AtsushiSakai/JuliaSamples/blob/master/JuMP/convex_opt/knapsack2.jlgithub.com

今回はなんとなくソルバーとしてCPLEXを使ってみました。

ソルバーオブジェクトの名前がCplexSolverであることに注意が必要です。

以前の結果と同じ結果が得られています。

ナップサック問題におけるcvxpyとJuMPの計算速度比較

Juliaは計算が早いことで有名な言語なので、

cvxpyとJuMPで計算速度のベンチマークを取ってみました。

下記がcvxpyのコード

#
# A sample code to solve a knapsack_problem with cvxpy
#
# Author: Atsushi Sakai (@Atsushi_twi)
#

import cvxpy
import numpy as np
import random
import time

N_item = 30000

size = np.array([random.randint(1, 50) for i in range(N_item)])
weight = np.array([random.randint(1, 50) for i in range(N_item)])
capacity = 1000

x = cvxpy.Bool(size.shape[0])
objective = cvxpy.Maximize(weight * x)
constraints = [capacity >= size * x]

start = time.time()
prob = cvxpy.Problem(objective, constraints)
prob.solve(solver=cvxpy.ECOS_BB)
elapsed_time = time.time() - start
print("elapsed_time:{0}".format(elapsed_time) + "[sec]")
result = [round(ix[0, 0]) for ix in x.value]

print("status:", prob.status)
print("optimal value", prob.value)

下記がjuliaのコードです。

using JuMP
using CPLEX

function main()
    println("JuMP knapsack")
    model = Model(solver=CplexSolver())

    nitem = 30000
    capacity = 1000

    size = rand(1:50, nitem)
    weight = rand(1:50, nitem)

    @variable(model, x[1:length(size)], Bin)
    @objective(model, Max, dot(weight,x))
    @constraint(model, dot(size, x) <= capacity)

    @time status = solve(model)
    println("Objective value: ", getobjectivevalue(model)) 
end

main()