目次
- 目次
- はじめに
- 双対問題とは?
- なぜ双対問題を考えるのか?
- 非線形問題における双対問題
- 線形計画法の双対問題を導出してくれるPythonライブラリdual
- 様々な最適化問題の双対問題まとめ
- より詳しい双対問題の説明を知りたい人は
- 参考資料
- MyEnigma Supporters
はじめに
最適化問題を勉強していると、
双対問題[そうついもんだい] (dual problem)という言葉が出てきます。
実は最近の凸最適化のソルバーなどが、
高速に問題を解けるようになったのは、
この双対問題という考えを使うことにより、
実現していることが多いようです。
今回、この双対問題の概要と、
なぜ双対問題を考えると、
最適化を解きやすくなるのかを
紹介したいと思います。
双対問題とは?
双対問題はある最適化問題(主問題)に対して、
補集合になる最適化問題のことを指します。
例えば、下記のような線形計画問題の場合、
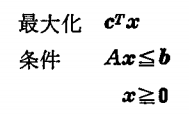
その双対問題は、下記のような問題を指します。
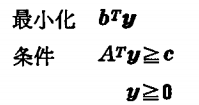
これは、
最大化問題では、最適値の上界(最小化問題)を求め、
最小化問題では、最適値の下界(最大化問題)を求めることになります。
このような双対問題は、
基本的にすべての最適化問題に存在するのですが、
複雑な最適化問題の双対問題は、上記のように
あまり式の対称性が無いものもあります。
例えば、下記の最適化問題において、
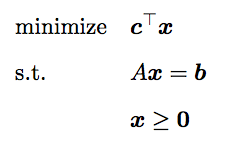
その双対問題は下記のようになります。
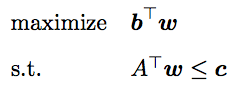
なぜ双対問題を考えるのか?
なぜ、この双対問題を考えるかといいますと、
この双対問題を考えることで、
対象の最適化問題を簡単に解くことができることが
多いためです。
例えば、上記の双対問題には、
下記の双対定理という定理が成り立ちます。
双対定理(英: duality theorem)
主問題と双対問題のいずれか一方が最適解を持つなら、
もう一方も最適解を持ち、主問題の最小値と双対問題の最大値は一致する。
つまり、解きたい主問題の最適値を計算するのが難しい時、
その双対問題を解くことで、主問題を解くことができることがあります。
(ちなみに相対問題を解くと、主問題も解くことができるのは、
線形計画法のみのようです)
例えば、主問題の変数がたくさんあり、制約条件が少ない問題の場合、
双対問題の方が変数が少なくできます。
すると、主問題より楽に解ける可能性が高いのです。
また、もう一つのメリットとしては、
最適性の簡単な証拠を提示できるというのがあります。
ある最適化問題の結果が、本当に最適値かどうかを確認する際に、
上記の双対原理を使うことで、
主問題の最小値と双対問題の最大値は一致した場合、
その結果は最適値であると証明することができます。
非線形問題における双対問題
前述の通り、双対問題を解くことで、
多くの線形計画問題の解を得ることができますが、
非線形問題の場合、双対問題を解いても
直接、主問題の解を計算することはできません。
しかし、この主問題と双対問題を
交互に実施することで、
徐々に最適値に近づけていくことで、
最適化を実施するアルゴリズムのことを
主双対内点法(primal-dual interior point method)といいます。
現在、二次計画法などのソルバーとしては、
この主双対内分法を使ったソルバーが一般的のようです。
線形計画法の双対問題を導出してくれるPythonライブラリdual
Pythonライブラリであるdualを使うと、
線形計画法の数式を記述することで、
その双対問題の数式を表示してくれます。
具体的な使い方は下記を参照下さい。
注意点としてpython3系のみで動きます。
様々な最適化問題の双対問題まとめ
代表的な最適化問題とその双対問題の式をまとめておきます。
線形計画問題 1
主問題
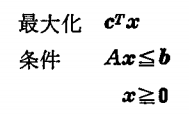
双対問題
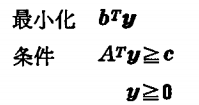
線形計画問題 2
主問題
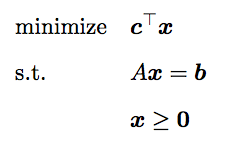
双対問題
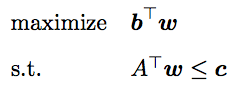
Second-order cone programming
主問題
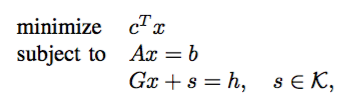
双対問題
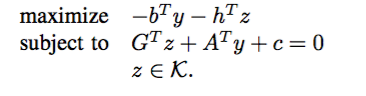
より詳しい双対問題の説明を知りたい人は
こちらの資料がおすすめです。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
