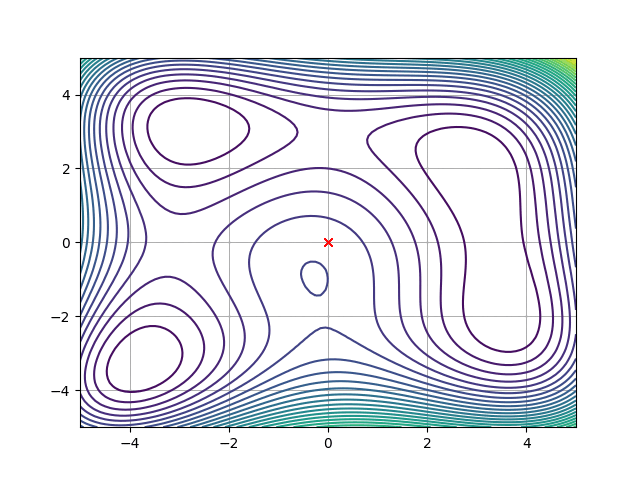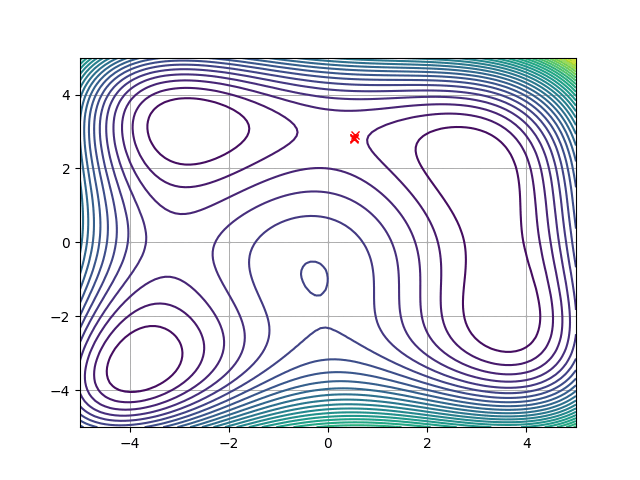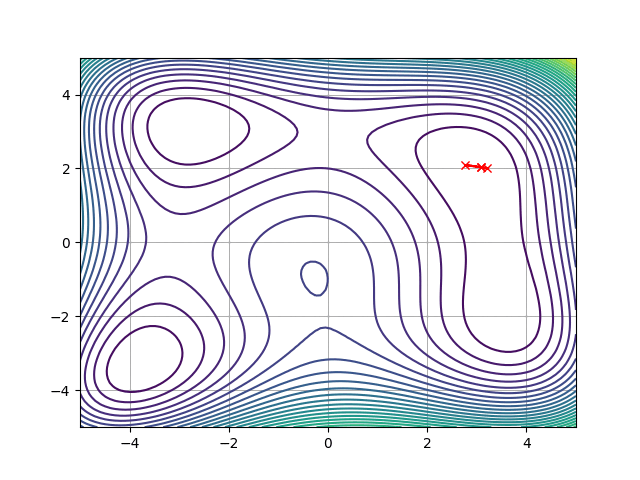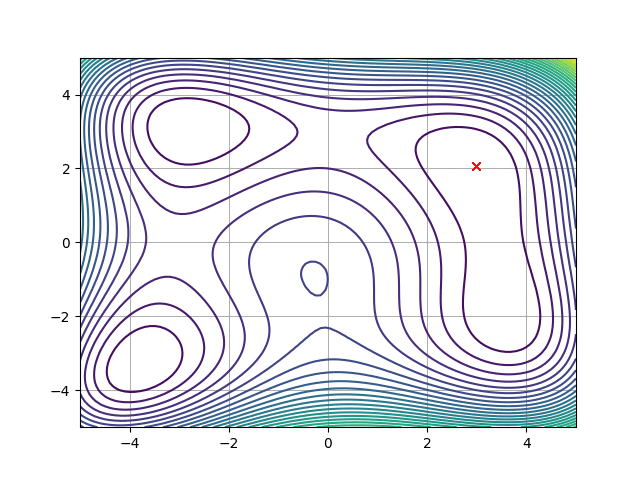
目次
Nelder-Mead法
Nelder-Mead法は、非線形最適化法の一種です。
シンプレックス法やアメーバ法とも呼ばれます。
このNelder-Mead法は、多角形の探索領域を
広げたり、縮小したり、移動させることにより、
多次元非線形関数の最小値を探索します。
Nelder-Mead法の特徴
一般的な非線形最適化手法は、
目的関数の微分情報を使用しますが、
目的関数が不明な時や、
目的関数が複雑すぎて微分出来ない時などには使えません。
このNelder-Mead法はそのような微分情報が無くても
非線形最適化を実施することができます。
一方で、
微分情報を使わないため、
収束計算に時間がかかってしまう時がある
という問題があります。
Nelder-Mead法の計算プロセス
0: シンプレックスの初期化
コスト関数の引数の次元をNとしたときに、
N+1個のシンプレックス(アメーバの頂点)を生成します。
冒頭の画像のような2次元(x-y)入力の場合は、
三角形のシンプレックスで最適値を探索します。
シンプレックスの点は、探索範囲の中でランダムに生成するか、
事前に最適値の範囲がわかっている場合は、
その周囲にサンプリングすることが多いようです。
このあとは1-5を繰り返し計算します。
1: 重心計算
最もコスト関数が悪い頂点Xw以外の、シンプレックスの重心を計算する。
この最もコスト関数が悪い点を、
これ以降のプロセスで移動させて最適化を実施します。
2: Reflection (反射)
Xwを重心を元に、反転させます。
その反転された点のコストが、最高でもなく最低でもない場合は、
反射した点を、Xwに置き換えて、ステップ1に戻る。
- 連続変数の場合のReflection式

- 整数変数の場合のReflection式


(重心とXwのコスト関数の絶対値差の次の整数)

- α: 整数重みパラメータ
3: Expansion (膨張)
Xrが最適な場合は、Xrを延長して、より最適解が無いかしらべます。
延長したものが最適の場合は、それをXwと置き換え、
元のXrの方が良い場合は、XrをXwと置き換えます。
- 連続変数の場合のExpansion式

- 整数変数の場合のExpansion式

4: Contraction (収縮)
この時点で、XrはXwより良いか悪いかを判断して、
良い場合は、Xrを内側に伸ばして、
悪い場合は、Xwを内側に伸ばして、
良くなった場合は、それをXwと置き換えます。
悪くなった場合は、Shrinkを実行します。
5: Shrink (全収縮)
ここではXwより良い点を見つけられなかったので、
一番良い点以外を、一番良い点に近づけます。

Pythonサンプルコード
import numpy as np def nelder_mead(func, x0, *, ftol=1.0e-8, max_iter=1000, callback=None): """ Nelder Mead solver :param func: The objective function to be minimized. :param x0: Initial x vector :param ftol: Relative tolerance for convergence. :param max_iter: The maximum number of iterations over which the entire population is evolved :param callback: A function to follow the progress of the minimization. Arguments are i: iteration count best_x: current best x best_obj: current best objective simplex: current simplex info :return: best_x: found best x, best_obj: found best objective """ x0 = np.asarray(x0) n = len(x0) if n < 2: raise ValueError("multivariate function is needed") elif x0.ndim != 1: raise ValueError(f'Expected 1D array, got {x0.ndim}D array instead') # parameters (adaptive scaling) alpha = 1.0 gamma = 1.0 + 2 / n rho = 0.75 - 1 / 2 * n sigma = 1.0 - 1 / n if max_iter is None: max_iter = 200 * n simplex = _initialize_simplex(n, x0) obj_list = np.array(list(map(func, simplex))) simplex, obj_list = _sort_by_objective_value(simplex, obj_list) x_g = np.mean(simplex[:-1], axis=0) best_obj = min(obj_list) prev_obj = best_obj for i in range(max_iter): f_best = obj_list[0] f_second_worst = obj_list[-2] f_worst = obj_list[-1] x_worst = simplex[-1] # Reflection x_r = x_g + alpha * (x_g - x_worst) f_r = func(x_r) if f_best <= f_r < f_second_worst: obj_list, simplex, x_g = _update(obj_list, simplex, x_r, f_r) elif f_r < f_best: # Expansion x_e = x_g + gamma * (x_r - x_g) f_e = func(x_e) if f_e < f_r: # f_e is better obj_list, simplex, x_g = _update(obj_list, simplex, x_e, f_e) else: # f_r is better obj_list, simplex, x_g = _update(obj_list, simplex, x_r, f_r) else: # Contraction if f_r <= f_worst: # f_r is better than f_worst x_c = x_g + rho * (x_r - x_g) else: # f_r is worst x_c = x_g + rho * (x_worst - x_g) f_c = func(x_c) if f_c < f_worst: obj_list, simplex, x_g = _update(obj_list, simplex, x_c, f_c) else: # Shrink # It brings all but the best points closer to the best. simplex[1:] = simplex[0] + sigma * (simplex[1:]-simplex[0]) obj_list[1:] = np.array(list(map(func, simplex[1:]))) obj_list, simplex, x_g = _update(obj_list, simplex) best_obj = min(obj_list) best_x = simplex[np.argmin(obj_list)] if best_obj < prev_obj: if abs(prev_obj - best_obj) <= ftol: break # converge prev_obj = best_obj if callback is not None: callback(i, best_x, best_obj, simplex) return best_x, best_obj def _initialize_simplex(n, x0): # initialize simplex # Ref: https://stackoverflow.com/a/19282873/8387766 h = lambda x: 0.00025 if x == 0.0 else 0.05 simplex = np.array( [x0] + [x0 + h(x0[i]) * e for i, e in enumerate(np.identity(n))]) return simplex def _sort_by_objective_value(x, ordering): indices = np.argsort(ordering) return x[indices], ordering[indices] def _update(obj_list, simplex, x_updated, f_updated): simplex[-1] = x_updated obj_list[-1] = f_updated simplex, obj_list = _sort_by_objective_value(simplex, obj_list) x_g = np.mean(simplex[:-1], axis=0) return obj_list, simplex, x_g def himmelblau(x, y): a = x ** 2 + y - 11 b = x + y ** 2 - 7 return a ** 2 + b ** 2 def main(): import matplotlib.pyplot as plt def plot_callback(i, best_x, best_obj, simplex): if i % 5 == 0: print(f"Iter: {i} f([{best_x}]) = {best_obj}") plt.cla() x = np.linspace(-5.0, 5.0, 100) y = np.linspace(-5.0, 5.0, 100) XX, YY = np.meshgrid(x, y) plt.contour(x, y, himmelblau(XX, YY), levels=30) sx = [x for x in simplex[:, 0]] sx.append(simplex[0, 0]) sy = [x for x in simplex[:, 1]] sy.append(simplex[0, 1]) plt.plot(sx, sy, "-xr") plt.pause(0.1) xopt, fopt = nelder_mead(lambda x: himmelblau(x[0], x[1]), x0=[0.0, 0.0], callback=plot_callback, ) print(f"Solution: f({xopt}) = {fopt}") plt.show() if __name__ == '__main__': main()
参考資料
【Python】Nelder–Mead method の実装と matplotlib による GIF 画像の保存 - Qiita
Nelder-Mead Optimizationcodesachin.wordpress.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
