目次
- 目次
- はじめに
- 線形サポートベクターマシン(Support Vector Machine:SVM)
- JuliaとJuMPを使った線形SVMの実装
- 非線形SVM
- JuliaとJuMPを使った非線形SVMの実装
- 参考資料
- MyEnigma Supporters
はじめに
今回は以前紹介した
凸最適化技術の応用例の中で、
最も有名なものの一つである
サポートベクターマシン(Support Vector Machine:SVM)の技術の概要と、
シンプルなSVMを実際に最適化ライブラリを使って
実装したコードを紹介したいと思います。
線形サポートベクターマシン(Support Vector Machine:SVM)
サポートベクターマシンは、
機械学習における分類アルゴリズムの一つです。
かなり古典的な手法ではありますが、
Deep Learningが出る前までは、
分類問題ではかなり精度が高いアルゴリズムであると知られていました。
凸最適化を使っているため、次元数の高い
画像などの分類問題も高速に計算でき、
局所最適値に陥らないため、
結果が安定しているという特徴があります。
また、線形分類問題の場合、
二乗誤差を最小化することで、同じように分類ができますが、
データの誤差などに引きずられてしまうという問題があります。
しかし、SVMはそのようなデータに強いという特徴があります。
SVMには、様々な実装があるのですが、
最もシンプルな線形SVMは
下記のような最適化式で表すことができます。
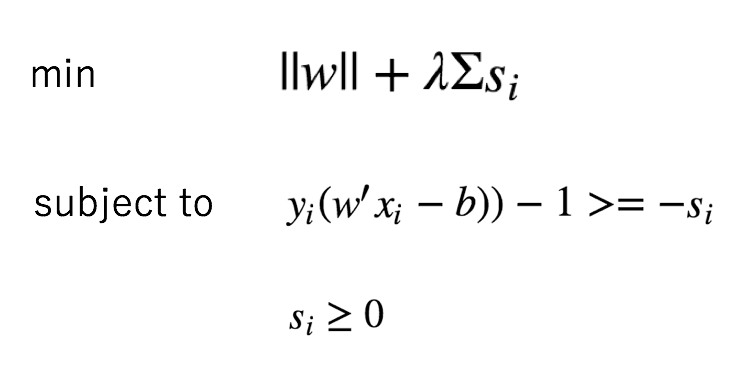
上記の最適化式において、
1/||w||は分類平面からのマージンなので、
||w||を最小化することで、分類平面からのマージンを最大化しています。
通常はLagrangeの未定乗数法を使って、
定式化することが多いですが、
今回は制約条件をそのまま使っています。
また、データが混ざっていても分類平面を計算できるように、
スラック変数を使って、制約条件を緩和させています。
(ソフトマージンSVM)
JuliaとJuMPを使った線形SVMの実装
ここでは、Juliaと、
Juliaの最適化ライブラリJuMPを使って
線形SVMを解くサンプルコードを書いてみました。
# # Linear Support Vector Machine sample with JuMP # # author: Atsushi Sakai # using PyCall using Distributions using JuMP using CPLEX solver = CplexSolver(CPX_PARAM_SCRIND=0) @pyimport matplotlib.pyplot as plt const λ = 1.0 function lsvm(x, y) model = Model(solver=solver) @variable(model, w[1:length(x[1,:])]) @variable(model, b) @variable(model, s[1:length(x[:,1])] >= 0.0) for i in 1:length(x[:,1]) @constraint(model, (y[i]*(w'*x[i,:] - b)) -1 >= -s[i]) end obj = w'*w + λ*sum(s) @objective(model, Min, obj) status = solve(model) w_vec = getvalue(w) b_vec = getvalue(b) println("w:",w_vec) println("b:",b_vec) return w_vec, b_vec end function main() println(PROGRAM_FILE," start!!") d1 = hcat(rand(Normal(-1, 2), 100), rand(Normal(5, 2), 100)) d2 = hcat(rand(Normal(1, 2), 100), rand(Normal(2, 2), 100)) d = vcat(d1,d2) c = vcat([1 for i in 1:100], [-1 for i in 1:100]) w, b = lsvm(d, c) seq = [i for i in minimum(d[:,1]):0.1:maximum(d[:,1])] plt.plot(seq, -(w[1] * seq - b)/ w[2] , "-k") plt.plot(d1[:,1],d1[:,2],"or") plt.plot(d2[:,1],d2[:,2],"ob") plt.axis("equal") plt.grid(true) plt.show() println(PROGRAM_FILE," Done!!") end if contains(@__FILE__, PROGRAM_FILE) @time main() end
x-y平面で、2つのガウス分布からデータを生成し、
それらを線形SVMで分類する線を決定しています。

上記のコードでは、スラック変数を使って制約条件を
緩和しているので、それぞれのデータが混ざっていても
分割線が引けていることがわかります。
非線形SVM
先程説明した線形SVMは、
二種類のデータを線形に分類することができますが、
非線形な分類はできません。
例えば、下記の左側のような2Dの点群の場合、
分類線は円で表現されるべきであり、
線形分類をするには無理があります。
しかし、下の右図のように、
この入力の点群をある関数で別の空間にマッピングすることで、
別の空間内では線形分類だが、元の空間では非線形に分類する手法があります。
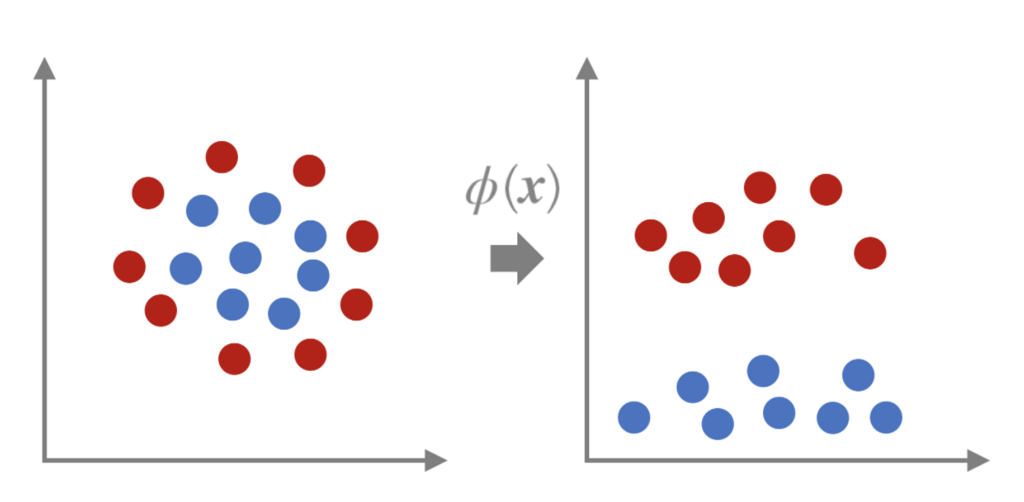
これを非線形SVMといい、
変換する関数をカーネル、
このカーネルを使う方法をカーネルトリックというようです。
このカーネルトリックをわかりやすく説明する動画として
下記があります。
カーネルとして使われる関数は、
多項式カーネルや、
ラジアル基底関数(RBF, radial basis function)カーネルなどが
有名なようです。
非線形SVMの詳細は
前述のリンク先の資料を参照ください。
JuliaとJuMPを使った非線形SVMの実装
続いて、前述のシンプルな非線形SVMを
JuliaとJuMPで実装してみました。
今回は、3つのガウス分布のデータを生成し、
その内2つのガウス分布のデータを一つのクラスタであるとしました。
残りの一つのガウス分布のデータはもう片方のクラスタとします。
このような場合、前述の線形SVMで分類するのは非常に難しくなります。
カーネルとしては非常にシンプルな二次多項式のカーネルとしました。
このカーネルを選んだ理由は特にありません。
このカーネルを使うことにより、二次元のx-yのデータが、
3次元のカーネル空間にリマッピングされ、
そのカーネル空間で線形SVMを解く形になります。
下記がJuliaのコードです。
# # Non linear support vector machine with JuMP # # author: Atsushi Sakai # using PyCall using Distributions using JuMP using CPLEX solver = CplexSolver(CPX_PARAM_SCRIND=0) @pyimport matplotlib.pyplot as plt const λ = 1.0 function kernel(x1, x2) y1 = x1^2 y2 = sqrt(2)*x1*x2 y3 = x2^2 return [y1,y2,y3] end function fit(x, w, b) if (w'*x - b) -1 >= 0 return true else return false end end function nsvm(x, y) model = Model(solver=solver) @variable(model, w[1:length(x[1,:])]) @variable(model, b) @variable(model, s[1:length(x[:,1])] >= 0.0) for i in 1:length(x[:,1]) @constraint(model, (y[i]*(w'*x[i,:] - b)) -1 >= -s[i]) end obj = w'*w + λ*sum(s) @objective(model, Min, obj) status = solve(model) w_vec = getvalue(w) b_vec = getvalue(b) println("w:",w_vec) println("b:",b_vec) return w_vec, b_vec end function main() println(PROGRAM_FILE," start!!") d1 = hcat(rand(Normal(3, 1), 50), rand(Normal(5, 1), 50)) d2 = hcat(rand(Normal(-3, 1), 50), rand(Normal(-5, 1), 50)) d3 = hcat(rand(Normal(1, 1), 100), rand(Normal(2, 1), 100)) d = vcat(d1,d2,d3) c = vcat([1 for i in 1:100], [-1 for i in 1:100]) nd = nothing for i in 1:length(d[:,1]) if nd == nothing nd = kernel(d[i,1], d[i,2]) else nd = hcat(nd, kernel(d[i,1], d[i,2])) end end nd = nd' w, b = nsvm(nd, c) seqx = [i for i in minimum(d[:,1]):0.5:maximum(d[:,1])] seqy = [i for i in minimum(d[:,2]):0.5:maximum(d[:,2])] for ix in seqx for iy in seqy if fit(kernel(ix, iy), w, b) plt.plot(ix, iy , "xk") else plt.plot(ix, iy , "ok") end end end plt.plot(d1[:,1],d1[:,2],"or") plt.plot(d2[:,1],d2[:,2],"or") plt.plot(d3[:,1],d3[:,2],"ob") plt.axis("equal") plt.grid(true) plt.show() println(PROGRAM_FILE," Done!!") end if contains(@__FILE__, PROGRAM_FILE) @time main() end
上記のコードを実行すると、
下記のような結果が得られます。
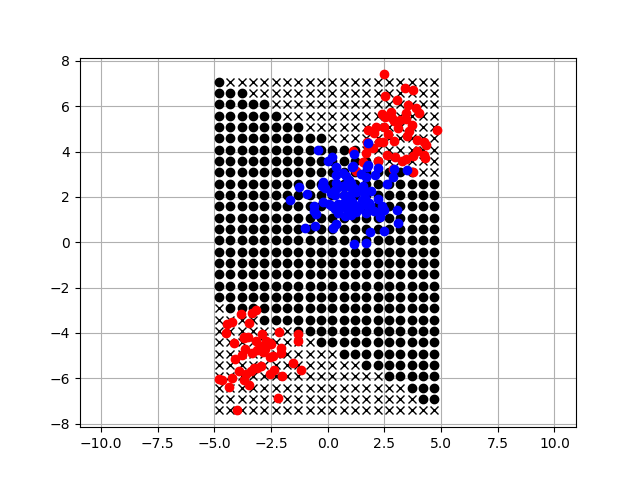
上記の図で、背景の黒い丸点とバツ点は、
非線形SVMで各点を識別した結果です。
領域の右上と左下で、
非線形に識別できていることがわかります。
この形状はカーネルの種類やパラメータにもよるのですが、
それっぽく識別できていることがわかります。
参考資料
MyEnigma Supporters
もしこの記事が参考になり、
ブログをサポートしたいと思われた方は、
こちらからよろしくお願いします。
