はじめに
下記の記事のように,
移動ロボットにおける自己位置推定(Localization)とは,
ロボットに搭載されている様々なセンサの情報から
ロボットの位置や姿勢を推定することです.
Localization (自己位置推定): 1 - MY ENIGMA
今回は,この自己位置推定法において,
デファクト・スタンダードになっている
確率的自己位置推定の概要について説明したいと思います.
確率的自己位置推定のイメージ
初めにこのような問題を考えます.
ある真っ直ぐな廊下があり,
その廊下の中でロボットが何処にいるかを知りたいとします.
ロボットは
タイヤの回転数から相対的な移動量と
カメラ画像から
自分が廊下にあるいずれかのドアの前にいるかどうかを
判断できるとします.
ロボット自身はカメラセンサを使って、
現時点において、廊下のどのドアの前にいるかはわからないとしますが,
事前に、廊下のどの位置にドアがあるかは知っているとします.
(廊下とドアのマップを持っている。)
まず初めに,
ロボットは,一番左のドアの前にいるとします.
しかし、ロボット自身は自分の場所を知りません。
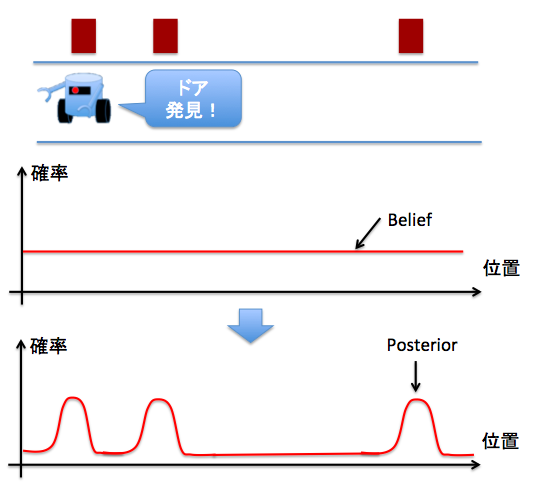
下記の図のように,
横軸に位置,縦軸に自分が存在するであろう確率をとると,
ロボット自身は,自分の位置情報を持っていないので,
ロボットの存在確率は
廊下のすべての位置で一様な分布になります.
続いて,
ロボットがカメラ画像から
"自分の前にはドアがある”
と認識したとしましょう.
(どのドアの前にいるかはわからないとする)
すると,
事前に知っているドアの位置情報から,
ロボットは現在,
3つあるドアの内のどれかの前にいる可能性が高いため,
存在確率は下記の図のように,
ドアの前の位置は上昇し,
その他の部分の存在確率は減少します.
ちなみに,
今回のドアの認識のような、
位置に関する外部情報のことを
一般的に観測(Measurement)といい,
観測により,更新(Update)する前の存在確率分布をBelief or Prior,
観測により更新された存在確率分布をPosteriorと呼びます。
続いて,
ロボットが右方向に移動したとします.
ロボットはタイヤの回転数から
移動方向と移動量を計算することができます.
(このような相対的移動量推定の方法をWheel Odometryといいます.
詳しくは下記の記事を参考にしてください
自己位置推定 (Localization):2 Wheel Odometry - MY ENIGMA)
すると,
下記の図のように確率分布も移動量の分だけシフトします.
そして,
続いてロボットが隣のドアを検知すると,
シフトされた確率分布が下記のように更新されます.
再び,ドアのある部分の存在確率は上昇し,
それ以外の場所は減少します.
この確率の更新方法に関しては、
ベイズの法則を使うことが多いです。
するとどうでしょうか?
はじめはロボットは位置がわからずに,
廊下のすべての位置で確率が一様でしたが、
複数の観測と移動の情報で
確率分布を更新することにより,
実際にロボットがいる場所(左から二番目のドアの前)
に確率分布のピークが生じて,
正確にロボットの位置が認識できていることがわかります.
これが確率的位置推定法です.
つまり,確率的自己位置推定法とは,
観測と移動の時系列情報を逐次的に利用して,
存在確率分布を更新し,
その時々に最もロボットがいると思われる場所を
確率的に推定することなのです.
今回の説明は、かなり抽象的で概念的な説明でしたが,
実際のロボットに搭載されている位置推定システムは
このアルゴリズムをより理論的に計算できるようにした方法である
カルマンフィルタやパーティクルフィルタを使用しています.
myenigma.hatenablog.com
myenigma.hatenablog.com
myenigma.hatenablog.com
今回の場合は,
観測の情報はドアの検知でしたが,
ロボットによって,それが電柱の位置だったり,
交通標識の位置だったり,
Google Carの場合は地面の白線の位置だったりします.
Sebastian Thrun: Google's driverless car - MY ENIGMA
しかし,大本になる考え方は,
すべてこの考え方に即しているといえます。