下記の記事で
ベイズの定理を用いた確率計算の説明をしました。
待ち合わせに遅れる彼女、ベイズの定理、そして例題 - MY ENIGMA
今回はこのベイズの定理を利用した
ベイズ統計学について説明したいと思います。
ベイズ統計学とは?
ベイズ統計学とは、
ベイズの定理における
事後確率と事前確率を
単純な確率(P=0.5など)ではなく、
確率分布として考える事により、
データを解析する統計学の一種です。
ベイズ統計学におけるベイズの定理
基本的にはベイズ確率論のベイズの定理と形は同じですが、
それぞれの項が意味するものが変わります。
下記のベイズの定理の式において、
P(A): 事前分布
データHが得られる前のパラメータAの確率分布
P(H): 正規化項(定数)
すべてのパラメータにおいてデータHが得られる確率分布
P(H|A): 尤度
パラメータAの時にHが得られる確率 (確率分布ではない)
P(A|H): 事後分布
データHが得られた時の、パラメータAの確率分布
を意味します。
つまり、
データHが得られるたびに、上記の式を使って
パラメータAを更新することにより、
データHの統計結果を
パラメータAの確率分布として表すことができるのです。
確率分布(確率密度関数)とは
確率分布とは、
それぞれの値になる確率を記述したもので、
その中でも確率分布が連続値となる場合の
確率分布を表した関数を確率密度関数をいいます。
この確率密度関数としては一番有名なのは
正規分布(ガウス分布)で、
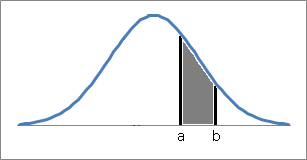
グラフ化すると下記のような形をしています。
確率密度関数の特徴として、
この確率密度関数の面積が確率を表すということです。
例えば、上記の確率密度関数において
0から1の値を取る確率は、
横軸の0-1の間の確率密度関数の面積になります。
ちなみに確率密度関数の場合、
0.0という値を取る確率は面積が0になるため、
理論的に0となります。
なぜなら確率密度関数は連続値を取るため、
0.000000000.....と無限に0が続くような
ある一つの値を取る確率は無いという考え方なのです。
一方で、0.00000000と0.00000001の間の確率は
非常に小さいながらも0にはなりません。
ベイズ統計では、このような確率密度関数を使用して
データを統計的に処理するため、
解析対象を確率的に取り扱うことができます。
ガウス分布(正規分布)の特徴
確率密度関数の中で最も有名なガウス分布は、
ガウス分布のパラメータである平均μと標準偏差σを使って、
データがどれだけの確率で出現するものなのかを計算することができます。
有るデータx'が
μ-σ
統計学とベイズ統計学の違い
ベイズ統計学では、
下記の記事で紹介したようなベイズの定理の利点を
統計解析でも利用することができます。
待ち合わせに遅れる彼女、ベイズの定理、そして例題 - MY ENIGMA
例えば、理由不十分の定理より、
事前確率の初期値に、
経験的な値(人間の勘など)を利用できますし、
新しいデータが追加された時に、
再び全部のデータを解析するのではなく、
ベイズの定理を使って逐次的に解析することができます。
また、不十分なデータにおいても、
経験的な知識を利用することで、
正確な分析をすることができます。
例えば、下記の記事がわかりやすいですが、
「ベイズ統計学」が分かりにくい理由 | 粉末@それは風のように (日記)
ベイズ統計学を利用することにより、
データの偏りがある場合でも正確な解析を行うことができます。
データに偏りがあっても、それを事前情報としておけば,
データの偏りによる推定の誤りに影響されることなく、
適切な分析(母集団)を計算することができます。